THE MATRIX a new concept of space

Part1: The Matrix of space

“No point is more central than this, that empty space is not empty. It is the seat of the most violent physics.” - John Archibald Wheeler

Abstract

In today's physics, space is seen as an existing thing, which, however, is no longer physical since Einstein. This but doesn't corresponds to pure logic, since a medium then must be defined as a separate thing in order to explain the strong cosmic forces of gravity. This would result, that all interactions have to be seen as separate particles which don't need a medium (particle zoo). Thus an abstract chasm arose between the electro-magnetic and the gravitational space. Of course, the interaction of gravity could not be seen as particles. This created in the minds of astrophysicists the deep belief that space is some kind of tough matter. Yet, inconsistently, the thing "space" was seen as emptiness on a small scale. The confusion is huge.

In Matrix theory, space and time is a phenomenon of the matrix, a harmonic and scalable structure of points that are in certain geometric relationships and form an equilibrium in all values (quantum number). These points are 4-dimensional oscillations between 4 values that can replace all quantum values in today's physics. So all particles are seen as properties of the matrix at that local point. Now there is no fundamental difference between particle and matrix. A particle is the 4-dimensional oscillation of this matrix. All properties of fields and particles are explained as parities of their oscillation. The physics of our world, space and time can be explained by this matrix. So there are no separate things, they are all just different constellations of the matrix.

The space

At the beginning of all ponderings, space is considered a container. In the empty state it is isotropic, it is empty everywhere. In the 19th century Maxwell gave space a meaning as a medium, the idea of ​​electro-magnetic space was born. He called it ether. It was also considered as isotropic. Maxwell relativized all movements in space to the ether. The speed of light had an absolute value that is the same everywhere in space. At the end of the 19th century Michelson was able to measure the speed of light at 299,853 ± 60 km/s. Since the measurement was made with an accuracy of ± 60 km/s, the light would have to be significantly slower in the direction of Earth orbit and faster relative to the measuring device towards orbit. Later the measurement accuracy could be inproved to ± 10 km/s (the earth speed is approx. 30 km/s). Thus the Maxwell theory of an ether lost its foundation and is based on a paradox. The Dutch mathematician Lorentz solved the problem mathematically with his transformations of the limmit of light speed for space and time. These show only minor differences from the classic values at normal speeds. They only take effect at speeds that were unattainable at the time. The young Einstein wanted to explain this effect explicitly and came to the conclusion that the ether can't have any physical values. This, however, differed his concept of space from that of Newton, Maxwell, Lorentz and Mach. Einstein was in a dilemma. On the one hand, the Einstein space modified the ways of measuring lengths, time and energies; on the other hand, space is not a medium with friction. He came to the strange conclusion that space only existed as a concept but not physically (without a medium) and can't perform any motion.

The empty space of Einstein

A physical space without any motions would be a rigid medium in which only propagation is possible. This medium should have two significant properties: It should be invisible and, despite the apparent emptiness, be able to transmit the greatest energies.

That would be the space, Einstein was looking for

Both properties would be created by space units (space-atoms). These atoms of space contain 4 centers of force in a geometrical constellation, which internally cancel each other out in terms of space, time and energy and add up externally to a zero unit. If one regards these centers as neutral space-atoms, then space would be without energy and appear as empty. If one looks at the interior of these space-atoms, then one sees immeasurable energies in a strongly condensed space and a large dilated time. In order to keep in balance and equilibrium of all values, these centers of force have to be in a certain geometric constellation.

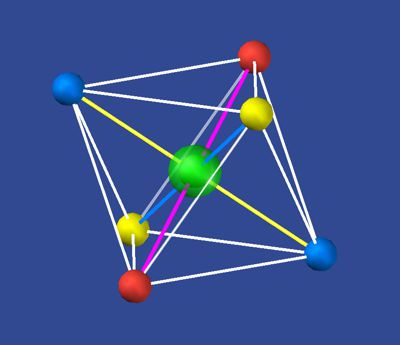
They are octahedra and tetrahedra

And this is how they are proven: Take a transparent plastic bag and fill it with glass balls. When the centers of these balls are connected to each other, you will find the matrix of space. This matrix is able to place the whole space with 4 colors in such a way that no color has a neighbor of the same color. Since these 4 colors are the symbols of properties, of the energy state and its temporal appearance, such a constellation as a group of four results in an equilibrium. It is transparent.

The philosophical background

As a shortcut: The matrix theory is based on harmony and balance of the primordial phenomena what generate space-time-pulses. These phenomena (axioms) are existing from the beginning, but because of their balance and equilibrium they form an emptiness, an invisible, non-interactive substance of empty space. Only the disturbances of this system create the reality space-time-pulse. In contrast to today's physics, the Matrix-Field-Theory (MFT) does not begin with an absolute chaos of a Big Bang Scenario but with an absolute harmony what forms an apparent void due to the equilibrium of the axioms of space-time-pulse. Empty space is not empty, it is a system of space-time-pulse that in the state of equilibrium, i.e. in perfect balance, has no effect outside of its system. When our universe was born, conditions prevailed that did not allow any asymmetries or disturbances of the system to survive.

Space is explained here by a geometric structure, the matrix,
Time by a full cycle of 360° from (+) to (-) as tensor at the 4th dimension and
Pulse is explained by the resistance to leave the original harmonic state.

This field theory has the advantage that it is a GUT (General Unified Theory) from the beginning and all further determinations from this point go like the branches from the original trunk, while classical science is a mix of experimental results and the search for theoretical affiliations is what often leads to different theories. Classical science thus has many planting sites that then try to unite in one trunk. The recognition of field theory would not overturn physics, but it would fundamentally change the image of the physical world. By 4-dimensional geometry of fields, its 360° cycles of time and its scaling, the matrix explains fermions, bosons, mass, inertia, charge, chromodynamics, gravitation etc.

The space dimensions

Spatial dimensions are utilities of our imagination. They become concepts of our intellect and mathematics. Now the question arises, are they real, are they physical? To understand this better, an example here is given:

The concept of dimensions starts with dimension zero (D0) and it marks a place. The place but is information, nothing else. The other dimensions therefore only remain information as long as D0 has no physicality. To make the dimensions physical, D0 must be physical. This happend, when it becomes a size in space. Its length is zero as long as it is not measurable. In multiplication, however, it will develop into a physical value. Now D0 becomes D1 in the vector multiplication and this becomes D2 in the same sense etc. Already D1 now has a thickness as D2 will have due to its physicality. D2 is not just a surface, it is like a sheet of paper with a backside (however thin it is). In 2D this is an indication of the existence of D3. In short: A dimension becomes a real physical quantity if it has indications of the next higher dimension. If we assume that our D3 space is real, then its physicality lyes in the 4th dimension.

The 4th dimension must therefore inevitably exist.

The vibration tensor to the 4th dimension

The space matrix with its hexagonal, orthogonal and trigonal aspects of its structure is hard to imagine. But how should the oscillation toward the 4th dimension be presented, especially why? Well, in the world of vibrating vectors, the higher dimensions cast their shadows on the lower ones. There are signs of transitions. D0 must have a size, even if this size is below measurability and remains unproved. A D1 line must have a right and a left side in order to transfer to the 2nd dimension. A surface D2 must have a backside to form the 3rd dimension. So D3 must have a direction of oscillation that uses all other oscillation values of the coordinates as a tensor field and also gives you a reality in a new dimension. In short:
We are real, even if our components are only vibrations.

The main problem with imagining the 4th dimension of space is that different things can have the same x, y, z values. 4 cubes in 4 colors with the same sizes in the same place x, y, z show us only one cube with one color. In D4 we would see 4 cubes in 4 colors. Unfortunately, the matrix as a geometric structure does not take into account our limited imagination. It simply determines there.

The matrix the fabric of space

The purpose of this space structure is, that an assignment of properties will cancel out each other, resulting in a space without any external value. As long as these properties cancel each other out as a sum of values in a space unit, these units can keep energies of any size and still appear to have no physical value outside. The physical space can carry the highest energies, where the properties of time and pulse cancel each other out in the sense, that time and pulse become these values here:
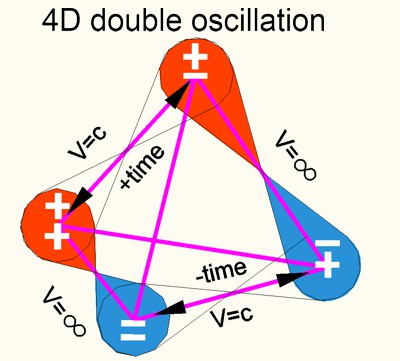
(+ +) = red, (+ -) = green, (- +) = yellow and ( - -) = blue
and therefore form an equilibrium by 4 colors. The exciting thing is that space itself can't get canceled out, even its units are null. Space becomes the main MEDIUM of our existence.

Within this tetrahedral-octahedral structure the balance of all properties is symmetrical. They exist but cancel out each other. Outside they exist only indirectly, they form a continuum of space-time-pulse. However, the space can no longer be seen as isotropic. It got neutral space atoms as physical carriers of its existence. From there on we have to get used to one thought:
our world no longer exists directly, only indirectly. We are the result of a medium and not separate of it. We are the modification of this medium, the disturbance of its equilibrium. Just like its components, our world is not chaotic either. The principles of these order were created when our universe was born. Unimaginable pressures prevented the inharmonious and chaotic from surviving this process. The Big Bang is nothing else than a peak of density, what forced anything to harmonic relations.

"What we see as material bodies and forces is nothing other than the forms and structures of space and time" - Ermin Schroedinger.
“Everything we see as real is made of things that cannot be seen as real” - Niels Bohr

Here now is the geometry of matrix presented. The main problem will be the presentation. How could such a part of space look like? How could it depicted?

This pix showes a true 3D constraction depicted as isometric view by the author. The spheres present the status of space with its 4 colors, the values of space-time-pulses.

The tetrahedron

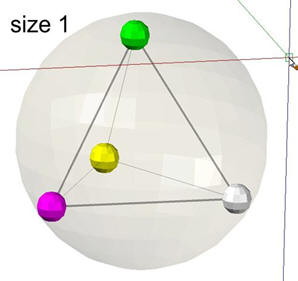
The tetrahedron is the most simplest 3D shape. It fulfills the condition creating a stable construction by the same distances between its 4 corners. To fix the distance, a scale (scale 1) S1 is assumed, which at the moment has no relation to a physical value. Further geometrical considerations refer to it. The 4 colors at the edges form the physical value of this space atom. They are intended as places, in which there are 4 field centers with 4 properties, which cancel each other out in every respect and result in a value zero at outside the system, the main condition of empty space.

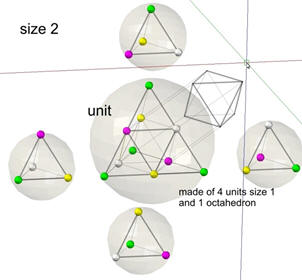
Since, according to the Planck formula, λ=h•c/E, where λ is the distance between field centers in S2 here have ½ of energy as in S1(scale 1). S1 as basis of all considerations therefore has the highest energy values. But S2 shows here that its edges are all at the same color, here green. A filled space with distances of S2 cannot hold energies locally as S1 does, they will spread with V=c. Here we come to one of the most important properties of "empty space". It turns out that all odd scales cancel each other out to zero (equilibrium) and all even scales like S2; S4; S6; etc. results as a medium for all forces where propagate with V=c, the medium for light or electric magnetic forces.

Even in a multiple application of tetrahedra, a space filling can be generated, where each property (color) finds its balance in neighboring fields.
The cycle includes 4 states of the space-force continuum, 2 of density and 2 states of time. This fact seduced physicists to assign a torsion (spin) or helicity (left / right) to fermions. The subject will be discussed later in more details.

The matrix of EMPTY SPACE therefore shows 2 properties in its innermost structure; one that can hold imaginable strong forces (S1; S3; S5 etc.) and one that allows the matrix acting as medium to spread all energies of space with V=c (S2; S4; S6 etc.).

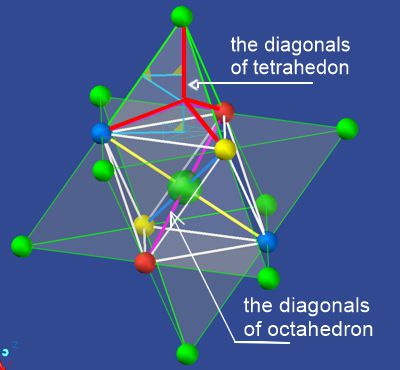
On closer inspection we discover that there is an octahedron inside the tetrahedron S2 (or as the picture shoes; S3 in S6). But since its corners are formed with the field centers of adjasing tetrahedra, the octahedron is only a space without content. An octahedron S2 would be in the intermediate zone of expansion anyway and would therefore only consist of field centers of the same color. They form not like S1; S3; S5; etc an equilibrium.
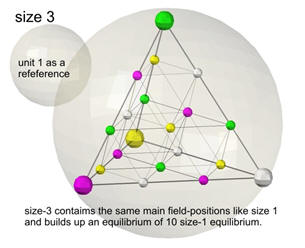
As a spatial form, size S3 has the same properties as S1. Since their rod sizes are 3 times longer than S1, they only interact with 1/3 the energy of S1.

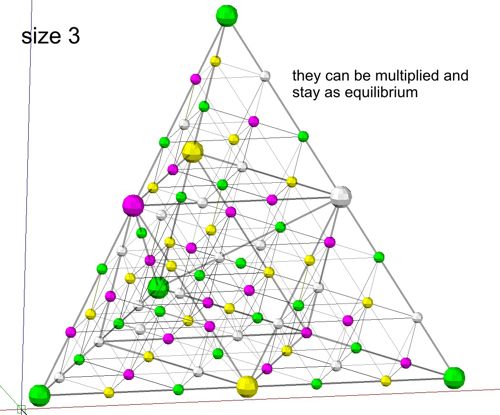As you increase the scale from S1 to S3, the octahedron spaces also increase. Since they also belong to the medium of the matrix, they also contain tetrahedra of size S1. The figure with side length S6 shows that the octahedron consists also of tetrahedra and octahedra inside.
From a purely geometrical point of view, each field center is connected 12-fold to its neighboring field centers. As can be seen later in our consideration of octahedra, it is very astonishing that despite the 12 bonds with only 3 neighboring colors (the relevant field center itself has already 1 color) no field center will have a neighbor with the same color. Space is filled with colors in such a way that they always cancel each other out to zero. Later we see that space is not a static construction, it oscillates from compression to decompression, in (+) time to (-) time and forms with the values (+ +)=red, (+ -)=green, (- +)=yellow, (- -)=beu,
the empty space.

Octahedron

It is not just an in-between space, it has properties that make it the carrier of our world. It is the seat of matter, while the tetrahedra are the medium.
Of course, tetrahedron and octahedron as spatial elements form a single structure which together does not leave any empty space. The space is thus completely geometrically defined. There are 2 octahedra + 4 tetrahedra per space unit. These have a volume ratio of 1 to 2 i.e. 1/3 volume tetrahedron and 2/3 volume octahedron.
However, these values have no direct influence on space.

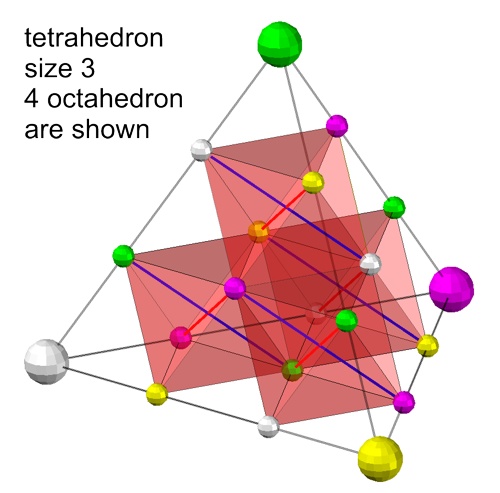
A calculation according to Pythagoras
(d=√(x^2 + y^2 + z^2)) would make little sense with this hexagonal spatial structure of the matrix, since a precise calculation here can only have integer values. The space is quantized by the requirement of connected scales. A tetrahedron with colored spaces is shown here. The octahedron in the center was covered with slightly transparent surfaces. The tetrahedra attached to the triangular surfaces represent the spatial properties as a medium. Here forces of spatial disturbances are passed on with V=c. In this case the resulting tetrahedron would have the size S6. The octahedron is size S3.

What is special about the octahedron?

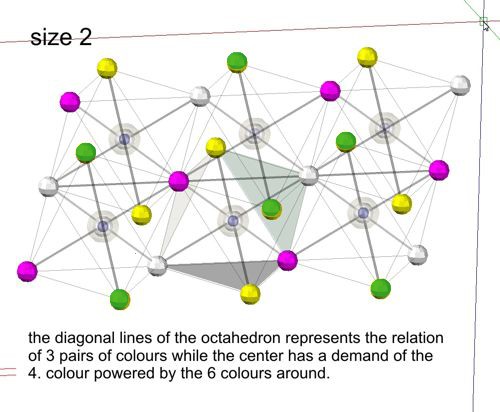If the surrounding tetrahedra are balanced, the octahedron is empty. If the tetrahedra are unbalanced, then a manko color in the center of the octahedron creates a moment of the 4th missing color in its surroundings. The diagonals are taken over as color from the neighboring octahedra and form, as seen left, a continuous orthogonal space. In this way, large spaces can receive moments and create areas of strength by these manko colors. This orthogonal space is stabilized by the flanking of each octahedron by twice the number of tetrahedra.

The disturbance of larger areas of space at the same scale creates the center in the octahedron, which creates an elastic resistance, resulting in force fields. These manifest themselves as onions shaped fields around each other in the length ratio of their distances (λ) 1; 3; 9: 27; 81 etc. or λ=3^x or 3^(- x). Thus, the octahedra result in a further property of space in addition to the above-mentioned property of an onion-shaped stratification of force-holding areas by uneven scales and force-emitting areas by even number scales.

Geometric Dates

The octahedron is characterized by 8 sides consisting of 12 edges of equal length and 3 diagonals. It is the connecting of 6 corners, which are the center for 6 spheres in 3 colors. Its vertices touch a parent sphere with radius r=√1/2=0.794. Despite the quite harmonious values, its color values are not in equilibrium. As part of a neutral, transparent medium and carrier of the highest energies, it must not have moments (colors) at its corners. As can be seen in the images above, the color moments shown here = zero. Energetically, they belong to the surrounding tetrahedra. The octahedron is a pure space-gap. Nevertheless, it has the spatial density of the antropy of its location. When this changes, a color moment is created at its center. We will soon see that an octahedron is less stable than a tetrahedron.

An abrupt disruption of the local entropy (experiments at LHC Geneva) mainly has an effect in its center, where the missing 4th color moment, the "manko color" appears. This manko color is produced by the color moments acting in the next higher scale, here green in the S2 scale, if the starting point for the octahedron is the S1 scale. At each surface (triangle) of the octahedron is a tetrahedron. There are therefore 8 tetrahedrons which, with the color moments of the octahedron and their apex, have the 4 color moments of equilibrium. A spatial structure is created which, in addition to the rigidity of the tetrahedra, has an elastic compensation zone in the spaces between them due to the octahedrons.

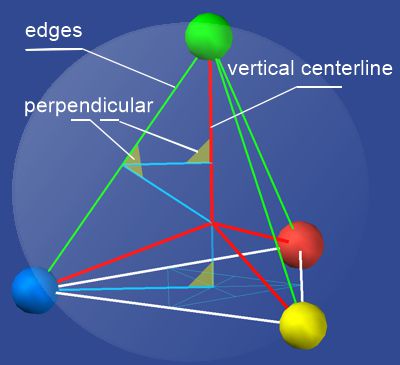Here briefly the geometric construction of the inner distances of a tetrahedron. We recognize 6 edges (3 green and 3 white, which the latter optically belong to the octahedron). We see the construction of its area midpoint in the white triangle (base). From there (perpendicular) is the vertical axis. The crossing point of a line drawn at right angles from the middle of an edge gives the volume midpoint of the tetrahedron. From there 4 (red) lines run to the corners, which then form the radius of a sphere touching all 4 corners of the tetrahedron. The radius of this sphere would then be 0.617 (side length=1). This shows that a tetrahedron is more stable than an octahedron (radius from the volume midpoint to the edges = √(1/2)=0.707) what means (<r=>E derived by (E=hc/λ)). In addition, the square basic shape of the octahedra is easily deformable, the forces (and thus the stability) are then conducted via the stiffer tetrahedra. The deformation of the space goes by the deformation of the octahedra. more details in my paper geometric analysis

Our universe, proof of 4 space-dimensions

Our universe is normally imagined as an expanding sphere. The spherical shape comes from our range of vision, which appears 13.6 billion light years in all x; y; z directions equally. The expansion is derived by the Hubble constant, which says that all observable parts of our universe move away from each other depending at their distance. That means approx. 70 km/s per Mpsc (Megaparsec). In other words: 2.2 km/s per 100,000 LY. So every 100,000 light years the speed of expansion increases. If it increases in 13.6 billion LY every 100,000 LY 2.2 km/s, then in the end it results in speed of light or V=c.

13.6 10^9/10^5 * 2.2 km/s = 13.6 10^4 * 2.2 km/s = 299 200 km/s

If the BB (Big Bang) or VB (Very Beginning) moves away from us with V=c, this means for us, not the VB but we are the ones who speed away by V=c. But this does not correspond to the SR (special relativity) and GR (general relativity). In the context of relativity the radial coordinate of this expansion would have zero and infinite values. We would  practically be flat and 2-dimensional. But that is wrong.

The solution offers the inclusion of the 4th spatial dimension in the account. From the prospect of 4th spatial dimension, our space would be a spherically curved surface (the curved space of Einstein), which propagates as an impulse wave with V=c in 4D hyperspace. All 3 spatial coordinates of our 3D space would remain in normal mode, but the 4D coordinate would then be invisible to us. A secondary effect would be that subatomic particles would have an oscillation of V<c in their 4D-coordinate.

It should be mentioned that Marco Pereira, MSc in Physics, PhD in Physical-Chemistry, based his extensive theory of a Hypergeometric Universe (HU) on this idea of a universe expanding in hyperspace with V=c. I wrote the first page of my matrix theory in 2016 as webpage. I saw the HU theory as an extensive confirmation. However, it was Billy Lee, free thinker, who drew my attention to the Hubble effect of V=c in relation to the size (13.6 billion LY) of our universe..

As we will see later, 4D-hyperspace is absolutely necessary as basis and carrier of our 3D world. However, its consequences in context of creation of our world are not discussed here. Here the existence of hyperspace should be shown as an important part of a matrix theory. It has 4 coordinates,  time is not counted. Time would be a human concept and not a spatial dimension. The Equation of relativity is written zero=(ct)^2-x^2-y^2-z^2 what means => ct (distance in c)= √x^2+y^2+z^2 and is therefore only a 3 dimensional vector. Time, however, is only an effect that we can see. Only from the point of view of the 4th dimension is it recognized that the universe, i.e. the entire coordination system, has moved on by ct. The universe has grown by ct during the distance d=√x^2+y^2+z^2.

A good proof of the paradox of our point of view is the fact that from us all distances point into the past, where galaxies are getting denser up to the CMB (Cosmic Microwave Background), behind which the Big Bang is 0.0003% of its distance. And that in all 360° by 360° directions. Consequence: We are in the center of the big bang. Solution: The Big Bang lies at the center of a 4D sphere whose surface is our curved space. Therefore, everything in our universe is equidistant from the Big Bang.

Einstein used time as an equivalent space coordinate to describe his math for a V=c dependent space. This still is correct in case of the space we see. In matrix theory, time is supplemented as a time with (+) and (-) values, because here it is not about the universe, but about the quantum worlds of  particles. There, time shows itself to be bound to cycles and separated from the universal time. However, a universal cycle of time should to be assumed in the sense of perfect harmony.

Euclidean, spherical, relativistic space

Of course there are more types of space concepts. They all struggle with the representation on an normal 2-dimensional paper. In principle, all 3 types of the above concepts can be polydimensional. Mathematically speaking, Euclidean space is a concept that corresponds to our normal understanding of space. Other spatial concepts can therefore also be represented as Euclidean. The description of  space also includes distances, areas, volumes and n-dimensional values. However, these are no longer the same for various concepts.

The Euclidean space

This spatial concept is based on an isotropic distribution of its units, which are infinit small spatial units. They are analog quantities, i.e. they can be divided as required. The distances are calculated by d=√a^2+b^2+n^2 where n stands for the coordinates of further dimensions. In this way, spheres, cones, etc. can be calculated. This type of calculation is sufficient for the vast majority of cases.

The spherical space

Although every sphere, i.e. a circle, a spherical surface, a spherical volume, etc. can be calculated in Euclidean terms, the results in spherical space are different. Its coordinates are all curved by π. This alone results in units of different sizes. Due to its curvature of co-ordinates, they become circles, spherical surfaces and curved n-dimensional spaces with infinit but limited coordinate lengths that are closed in themselves. The spherical space thus demonstrates in simple ways an infinite space of finite size, as is expected from today's prospect of universe size. Here is an equation overview that shows the influence of the spherical space concept in various dimensions. The designation D1, D2 etc. applies to Euclidean space with 1, 2, etc. dimensions. D1/D2, D2/D3 etc. applies to a measurement in spherical space with 1, 2, etc. dimensions, which in turn is embedded in an additional dimension (Dn+1). An intelligent being in spherical space Dn/Dn+1 does therefor not see the curvature, but only recognizes it indirectly through the result of its measurements.

The logical formula development here would be d1 = diameter; d2 = curved around the circumference; a1 = circular area; a2 = circle curved as a sphere; v1 = sphere volume; v2 is the curved spherical volume; w1 = the spherical 4 dimensional (4D) space; w2 = the curved 4D space or 4D surface in 5D space.

The calculation of the volume of our universe is about curved space (D3/D4). Although a curvature in  sense of π is considered idealized from a physical point of view, the equations give us a close approximation of the real values, which, as we will see in the following, only occur when determining the measurement to a location outside of the specified space concept. Curvatures of dimensional geometry can never be seen in its own dimension.

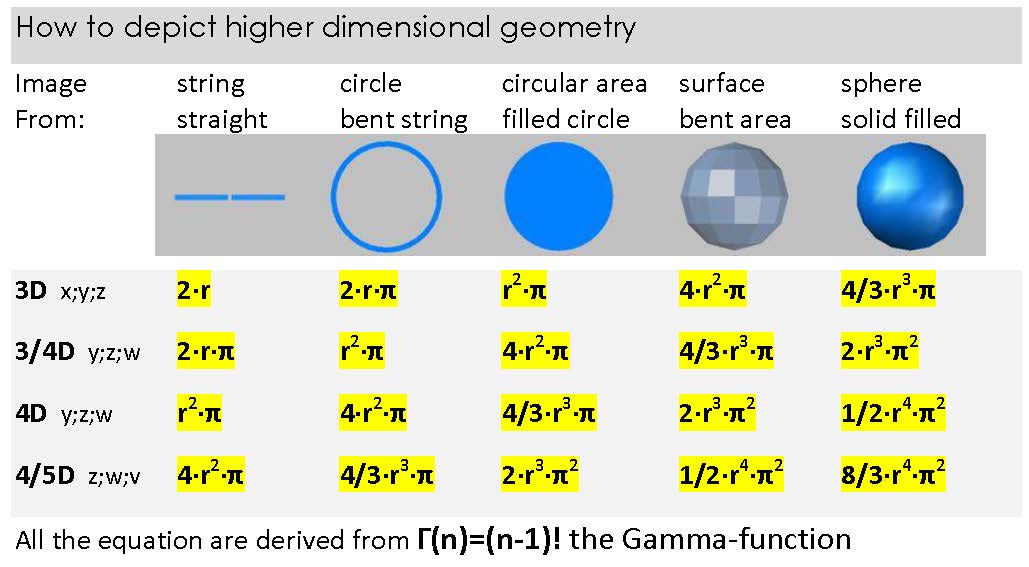
We humans are in the fortunate position of imagining 3 dimensions in 5 logical derivations of spherical space. These 5 derivations as 5 images have a logical dependency, the derivation of spherical quantities. There are 5 images that we can map over further dimensions, whereby the relationships between this spherical sizes also become visible in higher dimensions. Here's an example:

We consider the 4D space in the 4th dimension. The formula 1/2 r^4 π^2 is in the column of a solid sphere. The curved space is in the column of the sphere's surface, the 3D space is a filled circle, its surface is a circle, and a filled circle would then be a string.

A solid sphere as 4D space with a center (BB) would then have the curved (our) space as its surface, which in turn would be without a center and without boundaries.
Exactly this idea fits the situation of our research about our universe.

The relativistic space

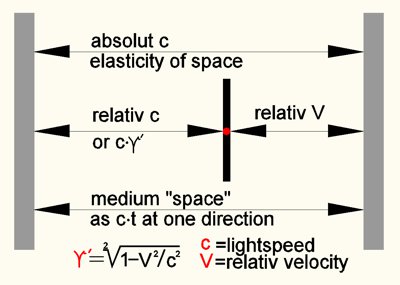While Euclidean space is isotropic and has equal units, spherical space has π curved coordinates, relativistic space consists of IV (intrinsic velocity) and LV (leftover velocity as c-IV). The problem, however, is that the IV is absolutely undetectable. If someone claims they have an IV=90%c (speed of light) that is their own choice, any other choice (e.g. 10%c) would also be true. In both cases, the LV would result in c. What actuely is the Lorentz metric? The Lorentz transformation was mentioned in the chapter "Space". Mathematician Lorentz developed of the fact that despite a significant intrinsic speed (IV) when trying to measure the speed of light, the same V=c always resulted forwards and backwards. He achieved this with his metric adapted to the IV. Here's an example (bei c=1 und IV=90%c) => ϒ''=1/ϒ): ϒ'' (Lorentz-Metrik) =
√(1-(IV/c)²) = √(1-(0.9/c)²) = √(1-0.81) = √0.19 = 0.435. The Lorentz metric ϒ'' is here 0.435

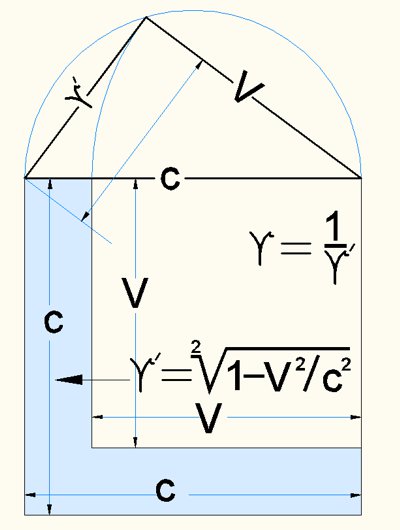left:

The picture shows Lorentz's considerations in a geometric context. The basis is the Pythagoras triangle with c as hypotenuse, IV and and ϒ'' as catheti. The upper values can be calculated with c²=ϒ''²+IV².
Below shows the same in context of faces.
Here it is shown that there is only one absolute speed, that of light. Since we and our measuring devices consist of oscillations with V=c, we remain relative. Our true speed remains a mystery to us. We can never know our IV or true LV (Leftover Velocity c-IV). We wouldn't notice if we were speeding through space by IV=90%c. It is the Lorentz metric, which adds each IV + LV to c. This applies to all dimensions that need the medium "space" to define it self. We see here that in the special theory of relativity it is only applicable for a vector (string size) and its time direction, in the general theory of relativity this also applies to the spatial density. Since the coordinate values (dependent on IV/c) create a different metric, entire spatial fields can of course also consist of small or large units, which can then be defined as spatial density. The relativistic space is therefore never isotropic.
To measure the speed of light, the result for any speed difference c-IV will result in c, because c is the speed of the mediums elasticity. According to Matrix theory, space is the medium with its internal structure, whereby the smaller structure is the medium of the larger one. The larger one but is the fabric of matter. Therefor matter is condensed space made of space in space.

The true nature of the MATRIX

The previous explanation of the matrix as a spatial structure gives rise to the feeling that despite its refined geometry and striking compatibility with modern quantum dynamics, it appears to be an arbitrary structure in inaccessible areas of physics for us. In the chapter "Our universe, the proof of the 4th space dimension" a scenario of a world generation is shown, which is based on facts of a whole century of observations of the universe, the Hubble constant. In 4-dimensional hyperspace, a spherical wave front arises from a center, which propagates into the future hyperspace with V=c. The representation here shows the hyperspace as 3D space, correspondingly our 3D space is presented as a wave front (geometrically a surface). The expansion in 4D space results in the Hubble constant in 3D space, e.g. 2.2 Km/s per 10·10^4 LJ. This would result in V=c at a distance of 13.6 billion light years. If V=c is seen as the medium speed, then it results in a visible universe of 2·13.6 billion light years as diameter. But this size of 27.2 billion LY is not only a distance, it is also a time back in past.
From our prospect we will see therefore at the end of this sphere as a hard shape or violant shiny surface, the beginning of every thing what is. We see not the end of our universe, but the end of time.

This is only explainable by higher dimension, what shurely are involved here. You have to look from the 4th dimension and imagian it as a 3 dimensional scene. Our universe will then be the surface of a 4D-sphere. And then, because of time-dynamic, you have to convert the beginning of time to the center of this sphere. The outer shape will be the "here and yet". You will be flat as a "flat earthler" living at the surface of this sphere. For you, the universe is endless and without a center. But to explain time, you need a center, a beginning. If you call this beginning as a Big Bang (BB), then it will be not found in your space, the surface. But you can see it by looking back in time. You will see the Cosmic  Microwave Background (CMB) and will know that just 0.003% behind this distance to you will be the BB.

You still wonder, how big is the size of our universe. You can find it by applying the dimensional formulas you could consult in: How to depict the higher dimensional geometry . The volumes of our bent universe is its 3D-volume (1/2)·(3/2π) = 2.36 *) times bigger. That is derived by the ratio of (2π^2·r^3) / (2·(4/3π·r^3)) or the equation of 4D-sphere / 2·3D-sphere (see the chapter: spherical space).
*) Each increase in dimension Dn to Dn/(n+1) doubles the size in addition to the bending, since the (+) size is then also accompanied by the (-) size. E.g. to the plain disc => spherical surface is the bending of the disc upwards and downwards. A disc in 3D space also gets a top and bottom side. This is applied in the chapter Hyper-space (matter/antimatter).
You will assume, 2.36 bigger in volume (v = r^3·4/3π = 13.6^3·10^27·4/3·3.14) = 10.535·10^30·2.36 LJ^3 will result in a 3D-radius of R=√3 ((v·3/(4π)) = 18.1 billion LY. That is but the radius of one revolving of an endless universe, not the radius of the bent space from the prospect in the 4th dimension. It can be described like this: The radius of a volume of a sphere in a curved space with r=13.6 billion LY is measured in the curved space lines as r=18.1 instead 13.6 billion LY. In a polydimensional representation (if the 4th spatial dimension is imagined as 3D), a sphere with r=18.1 billion LY must be expected.
How much dimensions you ever will need to explain complex scenes, the initialy radius r will never change. The V=c rule therefore are never violated.

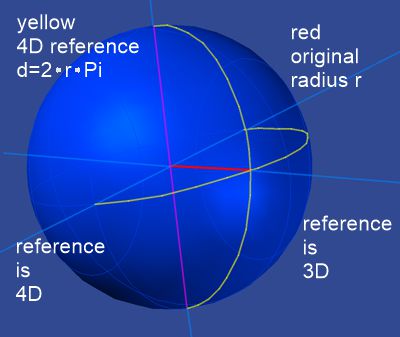Here appears some thing verry difficult to comprehend: In spheric geometry everything is bent by π except the initialy radius. Therefore the initialy radius can only applyed to the circle and the disc. At the surface of a sphere the radius is Rs = r·π, the initialy radius r is hidden. If the surface F=r^2·4·π is taken as a reference for 2D beings, then these beings recognize circumference/4 or R=r·π as their radius.
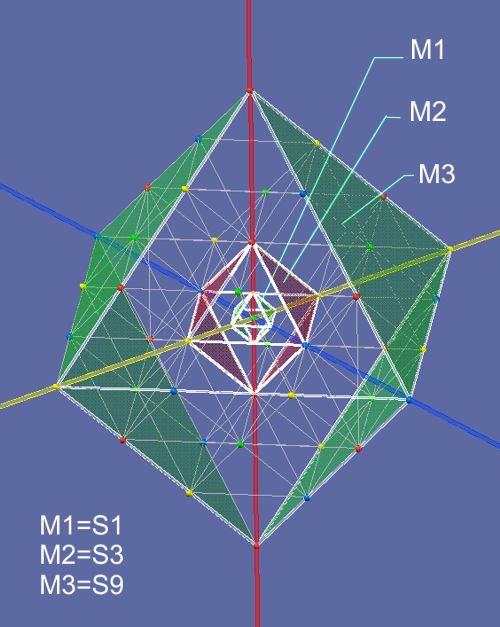
The image on the left shows the surface of 4D hyperspace, the size of which is not seen by us as 3D beings as r (red), but as R (the curved radius in yellow). Since this R is again in a curved space, it must be assumed that r=18.1 billion LY instead of 13.6 billion LY. R would then be r π = 18.1 billion LY 3.14=56.9 billion LY.

The size of our universe would thus have a radius 56.9 billion LY, wich generates a total size of 2·π·r = `114 billion LY, but still has from the prospect of 4D an initial radius of 13.6 billion LY. The rule of V=c will not be violated.

What would it mean for a super telescope? It could look in any direction in space and see the back of the observer's head after 2·π·r = 114 billion LY. In every direction !!! That would make a lot of heads. If now the time and the Hubble constant were included in the calculation, however, then we would never be able to see the size of our universe, it would flee from us faster than V=c. This is pure Geometry. There is no extra creation of space necessary. The raison-cake-theory is only good for children's fairy tales. Further considerations are left to the reader.

The purpose of this consideration is to understand the deep nature of the MATRIX geometry. Every momentum with vector of the 4th dimension would result in a point size in 3D. This would have a local disposition in 3D space with a tensor value from 4D. Only from here would this momentum result in local, standing waves in 3D space. Because such momenta oscillate during theire propagation through 4D space (with V=c), the standing waves become standing oscillating fields.

These local spatial points as oscillation and surrounded by their fields take over the geometric spatial pattern of the 4D space as momenta and transfer it 1:1 into 3D space. Their propagation in 4D structure has an effect in 3D space as a time cycle and thus creates the 4 types of effects in 3D space (++) (+ -) (- +) (-). These effects and the structure of the 4D space are the basic elements of MATRIX.

At Christmas 2016 I started to put my idea of a space matrix on the web. In 2017 and 2018 the ideas in my head and my 3D CAD platform grew into a zoo of solutions that required a logical order. In July 2018 I started to document these ideas in logical order with Word and pictures. The individual topics actually produced themselves and stunned me with their surprising solutions.

Gunter Michaelis, Griesbach, den 20.8.2020