Die MATRIX des Raum-Zeit-Kontinuums

Die Matrix des Raum-Zeit-Kontinuums

Eine Betrachtung des euklidischen Raumes bis zur mehrdimensionalen Existenz.

Die Werte des 3 dimensionalen Raumes sind hier Vektoren Werte
Die Werte der 4. Dimension sind hier als Tensoren oder Zeit bezeichnet
Mit MATRIX wird hier als eine 3 dimensionale Struktur bezeichnet
Der Begriff hex-metrisch bedeutet hier eine Metrik von 60°-Winkeln.

Wenn drei Dimensionen euklidisch sind, ist die Zeit ein imaginärer Wert. Es ist ein Tensor zu jedem Raumpunkt. Wenn die Zeit als Raumdimension betrachtet wird, könnte man den Raum auch als euklidisch betrachten, hätte jedoch vier Dimensionen. Dies erweist sich die bessere Theorie als der euklidische 3D-Raum mit einem Tensor in jedem Raumpunkt.

3D-Zeit-Äquilibrium = Null = √tc²-√x²-√y²-√z²-√4d² (die Einstein Formel)
auch als Grenzen des 4 dimensionalen elektro-magnetischen Raumes bezeichnet.

tc = Zeit · Lichtgeschwindigkeit = λ = Wellenlänge als Distanz, hier die max. Distanz aller Werte.

Ein 4D-Raumpunkt besitzt Zeit als 4D-Koordinate. Um Zeit als Koordinate betrachten zu können, bekäme sie die Freiheit zweier Richtungen. Vergangenheit und Zukunft hätten gleichberechtigte Existenz, was gegen das Causalitäts-Prinzip wäre. Vergangenheit und Zukunft wären daher nur dann frei zugänglich, wenn diese aus einer höheren Dimension (5. Dimension) kontrollierbar wären (Parallel-Welten). Das "Grossvater-Paradox" wäre daher nur denkbar, wenn eine Kontrolle der Zeitreise angewand wird. Diese aber wäre nur mit einem Wechsel der Zeitlinien möglich. Der Zeitreisende müsste in eine parallele Zeitlinie steigen, denn nur diese Freiheit der Entscheidung könnte er kontrollieren. In dieser jedoch wäre er trotz seiner Untat heute nie geboren worden.

Zeit als eine 4D-Koordinate mit allen Konsequenzen der 3D-Koordinaten würde keine erzwungene Zeitlinie erzeugen. Zeit ist daher eine im kosmischen Massstab begrenzte Koordinate, die durch einen übergeordneten Zyklus mit Initial-Punkt (Ur-Knall) beginnt und als radiale 4D-Koordinate unser Universum expandieren lässt. Der 3D Raum ist daher ein radial expandierender Raum in die "Zeit", die zur gleichenzeit auch Distanz (vom Urknall) bedeutet.

Die Physik der 4D-Räume kann nicht mehr isotrop sein. Es wäre ein 4D-Raum aus Energie. Diese bestände aus Schwingungen und die Schwingungsgrösse würde Felder bestimmter 3D-Grösse erzeugen. Eine Feldgrösse wäre die Wellenlänge λ oder ein Mehrfaches davon und somit eine Wellenfunktion (Schrödinger). Folglich sollte die Zeitkoordinate in gleicher Weise berücksichtigt werden. Das heißt, es fließt als 4D-Welle mit dem gleichen λ-Wert der 3D-Welle und wechselwirkt in dem Sinne, dass die 3D-Felder nun in Energie E und λ als Felder der Raum-Zeit existieren.

Der Raum ist hier nicht nur ein Konzept, sondern physikalisch existent. Der Raum als physikalisches Medium aber ist transparent. Das erfordert ein vollständiges Gleichgewicht aller 4 Quantenzustände, die Dirac formuliert hat. Alle Störungen würden sofort in den ursprünglichen Zustand eines Äquilibriums mit V=c zurückspringen. Dies gilt auch für alle betrachteten  Dimensionen. Während sich die Energie mit V=c fortbewegt, hat die 4. Dimension auf diese Weise auch einen lokalen Einfluss auf das 3D-Netz wie die 3D-Koordinaten es untereinander ebenfalls haben.

Die Energie als Raumeigenschaft des Mediums übersteigt unsere Maßstäbe. Alles, was wir messen können, ist die Energie seiner Störung. Auf diese Weise können wir niemals das Medium selbst verändern. Das physikalische Medium Raum ist im Grunde dasselbe wie seine Störung, jedoch jenseits jeglicher Manipulationsfähigkeit. Daher gibt es keine Unterscheidung zwischen Raum und seinem Medium. Unterschiede bestehen nur im Maßstab oder im λ seiner Grundfrequenz. Eines der grössten Schwierigkeiten in der Beschreibung des 4D-Mediums "Raum" liegt darin, dass alle Frequenzen als Gleichzeitigkeit gesehen werden und somit als λ ohne Zeitbegriff gelten.

Als Analogie gilt hier die Filmrolle, gerollt werden alle Sequenzen zu Längen ohne Bewegung. Erst das Abrollen im Projektor lassen Bewegung erkennen. Im 4D-Raum liegen die 3D-Räume übereinander, erst die Grundfrequenz unserer Erkenntnis lassen diese als ein 3D-Raum mit Bewegung erkennen. Der Unterschied, Zeit als 4. Koordinate zu sehen liegt in der Gleichzeitigkeit aller Zeitsequenzen, sodass wir in (-) als auch in (+) Werte gehen können.

Jedes λ erzeugt sein eigenes Feld oder besser gesagt, seine eigene Verschränkung. Jede Interaktion basiert auf demselben λ oder demselben Maßstab. Einzelne Felder erzeugen sekundäre Felder in größeren Maßstäben. Aus geometrischen Gründen gehorchen diese Sekundärfelder mit gleichem Mittelpunkt und ganzzahligem Größenfaktor (λ) der Maßstabsregel x = 3^x. Auf diese Weise interagiert z.B. ein Elektron mit einem Proton in einem 27-mal größeren Maßstab als das Proton.

Nach all diesen Konfigurationen erfordert die Logik, dass Punkte im Raum in bestimmten geometrischen Beziehungen platziert werden. Es gilt die Regel, dass alle Abstände (λ) im gleichen Maßstab gleich sind. Alle Raumpunkte haben den gleichen Abstand voneinander. Wir können mit der einfachsten Form beginnen, um den Raum geometrisch zu füllen. Betrachten wir zunächst die Konstruktion eines Würfelraums.

Bild 1

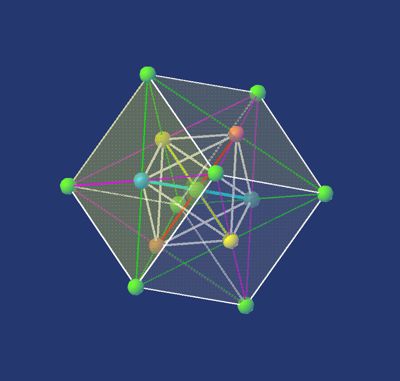
Es ermöglicht ein rechteckiges Muster aus Punkten; die einzelne Zelle wäre ein Würfel. Auf diese Weise werden 3 Dimensionen markiert. Um einen Weg zu finden, die Zeit als Schwingung durch die gleichen Würfel-λ- oder Punktabstände zu markieren, verwenden wir für jeden Punkt 2 Farben. Jeder Punkt hat zwei Zustände oder Paritäten seiner Schwingung. Ein solches Medium aus Würfel ohne Diagonalen würde leicht in alle Richtungen des 3D-Raums kollabieren. Nur die Zeitkoordinate wäre stabil. Alle Störungen würden die innere Konstruktion aufgrund ihres rechtwinkligen Impulses zum Hauptmuster verbiegen. Um dies zu vermeiden, wenden wir im Inneren des Würfels eine hex-metrische Struktur an. Wenn die Punkte an den Würfelkanten mit dieser Struktur verbunden sind, ist er stabil.

Das Bild 1 zeigt einen Würfel in einer hex-metrischen Raumstruktur. Der Hauptunterschied besteht darin, dass alle Punkte des Würfels die gleiche Farbe haben. Die Farben hier werden geometrisch von einem hex-metrischen Muster im Würfel abgeleitet. Das bedeutet einfach, dass die Abstände des Würfels nicht zu dem Massstab des hex-metrischen Musters passen und sein λ um √2 größer ist und daher keine zeitliche Beziehung oder Resonanz zum ursprünglichen λ seiner inneren hex-metrischen Struktur hat. √2 ist eine reelle Zahl, interaktiv können jedoch nur integer Zahlen sein. Die Eckpunkte sind untereinander nicht interactiv.

Betrachten wir nun das hex-metrische Muster. Die einfachste geometrische Form ist der Tetraeder. Warum? Stellen Sie sich vor, Sie haben 100 kleine transparente Kugeln in einem transparenten Plastiksack. In der Mitte jedes Balls befindet sich ein LED-Licht. Wenn Sie alle LED-Leuchten verbinden, erhalten Sie ein hex-metrisches Netz aus Tetraedern. Das liegt daran, dass Tetraeder den Raum (hier den Sack) am dichtesten ausfüllen. Das Ergebnis ist: Jeder Mittelpunkt jeder Kugel hat den gleichen Abstand zueinander. Die Anzahl der Zentren pro Raumeinheit ist höher als bei einer Füllung mit Würfeln. Der Grund, warum Wissenschaftler diese Idee nicht mögen ist, dass es einfacher ist, mit rechtwinkligen Koordinaten zu rechnen.

Bild 2

Würfel sind am einfachsten zu berechnen und erfordern nur zwei Farben, um die Bedingung der vollständigen Farbbalance zu erfüllen. Aber die Natur (und die Physik) geht den umgekehrten Weg und ordnet den Raum hex-metrisch an.

Beim Blick auf die kombinierten Tetraeder erkennt man, dass trotz der max. Dichte zwischen ihnen Lücken in Form von Oktaedern gibt.

Links: Blau sind die Tetraeder zum offenen Raum, Rosa symbolisiert hier eine Lücke zwischen Tetraedern, die hier ein Oktaeder darstellt. Wir müssen uns bewusst sein, dass Oktaeder nicht wirklich physisch existieren, sondern Lücken sind. Die Knoten dieses hex-metrischen Netzes gelten für Tetraeder und Oktaeder gleichermaßen. Nicht die Abstände (λ) machen das Medium des Raumes aus, es sind die Knoten des Netzes, was die physikalische Existenz des Raumes ausmacht. Ein Netzwerk aus Oktaedern oder Tetraedern ist nur eine Sichtweise.

Bild 3

Lasst uns nun die Geometrie des hex-metrischen Netzes analysieren.

Wir wissen, dass die Knotenpunkte gleiche Abstände haben. Dadurch entstehen gleichseitige Dreiecke. Wir erkennen, dass Oktaeder und Tetraeder aus den gleichen gleichseitigen Dreiecken bestehen. Tetraeder bestehen aus 4, Oktaeder aus 8. Addiert man auf den inneren Oktaeder-Flächen (rosa) 8 Tetraeder, so ergibt sich das Bild 2. Die äussersten Eck-Punkte dieser Konstellation sind die Eckpunkte eines Würfels (siehe Bild 3). Um diese Eck-Punkte zum Würfel aufzufüllen, werden 12 Oktaeder-Viertel, die Teile a; b; c der 3 anderen Oktaeder (4﮲a + 4﮲b + 4﮲c) benötigt. Die ¼ Teile ergeben zusammen 3 Oktaeder + 1 (der mittlere in Rosa) = 4 Oktaeder. Da die Referenz ein Würfel mit λ=√2 ist, wissen wir, dass 4 Oktaeder + 8 Tetraeder ein Volumen V=(√2)^3 sind. Jetzt berechnen wir das Volumen eines Oktaeders mit λ=1 als Voct=1·1·√2/3, subtrahieren 4·Voct und dividieren das Ergebnis durch 8 und erhalten Vtetra, das Volumen eines Tetraeders. Das ist nicht allzu schwer. Nun stellen wir fest, dass das Volumen des Netzwerkes zu 2/3 aus Oktaedern und zu 1/3 aus Tetraedern besteht. Dieses Verhältnis wird in allen Maßstäben gefunden. Es ist der mit 3 Dimensionen aufgebaute Raum.

Diese Überlegung gilt für den euklidischen 3D-Raum. Ein echter 4D-Elastik-Biege-Raum kann nicht starr sein. Zum weiteren Verständnis wird auf die obige Raumbeschreibung verwiesen. Stellen wir uns den euklidischen Raum als eine Ebene eines starren, aber 4D-euklidischen Raums vor. Da der 3D-Raum in dieser Sicht eine Ebene ist (3D-Ebene), können wir uns den 4D-Raum leicht als Volumen vorstellen. Ich werde es das 4D-Volumen nennen. Es wird wie oben beschrieben mit dem hex-metrischen 3D-Netz gefüllt.

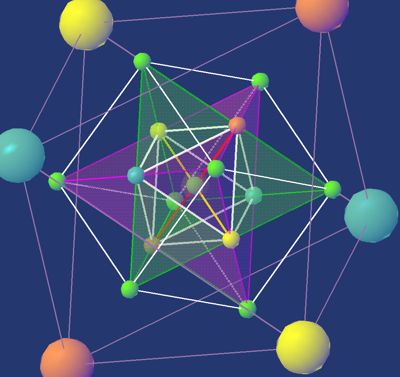
Die Zeitkoordinate fehlt. Zeit ist hier nicht die 4. Dimension; es ist eine Auswirkung davon. Um dies zu verstehen, müssen wir Distanz nicht als Länge im klassischen Sinne betrachten, sondern als eine Ganzzahl von Wellenlängen, die als reale Länge in einer Wellenfunktion erscheinen, einer Linie aus nicht reellen Punkten von Nullzuständen. Zeit ist in diesem Sinne ein Zustand einer Schwingung in einer bestimmten Gleichzeitigkeit. Diese Gleichzeitigkeit ist eigentlich ein Nullwert, ein Punkt höchster Präzision und verschwimmt, wenn die Zeit einen höheren Wert als λ hat. Aber dieser Zeitwert ist eine Länge, eine ganzzahlige Anzahl von Wellenlängen λ, der die Zeit in Einheiten quantisiert. In dieser Sicht sind Zeiteinheiten Wellenlängen in allen 4 Koordinaten, Linien aus Nullzustands-Punkten.

Bild 4

Es ist die Gleichzeitigkeit, die unser auf drei Dimensionen begrenztes wissenschaftliches Verständnis prägt. Nur traditionelle Gewohnheiten zwingen uns, Zeit als Erinnerung oder Zukunft zu interpretieren. Erweitern wir diese Gleichzeitigkeit auf die 4D-Koordinate, wird die Zeit zu einer realen Koordinate. Es wird genau wie die 3D-Längen zu einer Länge in Richtung eines 4D-Raums quantisiert. Längen in allen Dimensionen sind daher auch Zeiteinheiten, ihre Gleichzeitigkeit gilt als Quant.

Wenn wir das 4D-Volumen betrachten, was ist dann die Zeitangabe in einer 3D-Ebene? Das 4D-Volume hat definitiv keine Geschwindigkeit und daher keine Zeit. Es klingt ziemlich ähnlich wie Einstein in seiner Rede 1919 in Leiden: „Der Begriff der Bewegung sollte nicht auf ihn (den Raum) angewendet werden.“ Um dies auf unser 3D-Raumverständnis umzuwandeln, verwenden wir die hex-metrische Struktur, die jetzt als MATRIX bezeichnet wird, und fügen den Ecken der Tetraeder vier Farben hinzu.

Wir wissen, dass alle Koordinaten als Linien von Nullpunkten in Wellenlängen λ gesehen werden können. Man kann sie als oszillierende Felder bezeichnen. Die Matrixstruktur benötigt 4 als Farben markierte Paritäten, um die Anforderung eines perfekten Gleichgewichts zu erfüllen. Der Raum ist somit mit 4 Farben in der Art gefüllt, dass kein benachbarter Punkt die gleiche Farbe hat. Auf diese Weise leiten wir den Nullzustand bzw. den LEEREN Raum ab. Wir leiten dies durch einen Zyklus mit einer Doppel-Parität ab. Eine (+-) Parität in einem Grundzyklus in einer (+-) Parität eines überlagerten Zyklus. Symbolisiert als + +; + -; - +;  - -.

Bild 5

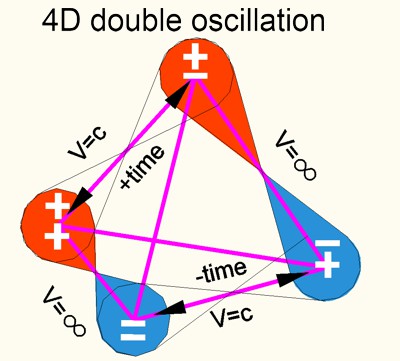
Es zeigt links oben ein Tetraeder mit den 4 Farben. Mitte: eine horizontale Oszillation aus 4D und senkrecht dazu eine 2-fache Oszillation im 3D-Raum als 1/2 Spin-Zyklus. Rechts unten werden die Farben als 4 Kombinationen von Rot (+) und Blau (-) dargestellt. Da sich der 3D-Raum bei der energetischen Einwirkung aus 4D (Tensor) zusammen zieht, ergeben sich die folgenden 4 Kombinationen:
1. max-Impakt aus (+) 4D = max-Kompression in 3D
2. min-Impakt (Null) 4D = max-Ausdehnung in 3D
3. max-Impakt aus (-) 4D = max-Kompression in 3D
4. min-Impakt (Null) 4D = max-Ausdehnung in 3D.
Ein 4D-Zyklus (360° = zwei 3D-Zyklen (180°) oder 1/2 SPIN in der Physik.

Bild 6

Nun stellt sich die Frage, wie ein Koordinatensystem aussehen könnte. Auf den ersten Blick sollten 6 Koordinaten mit 60° Winkel zueinander eine Lösung bieten. Alle Längen hätten dann ganzzahlige Zahlenwerte, da die Matrixstruktur keine reellen Werte zulässt. Dies wäre ein aufwändiges Verfahren, das mit den vertikalen Koordinaten des klassischen Raums nicht konkurrieren könnte.

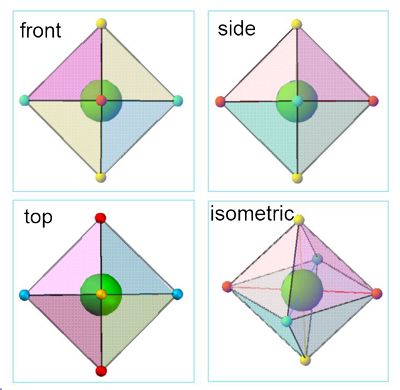
Oktaeder scheinen hier eine Lösung zu zeigen. Die klassische Darstellung Drauf-, An- und Seitenansicht zeigen, dass ein Oktaeder immer ein Quadrat bildet. Es wäre ein Koordinatensystem mit 3 separaten x;y Referenzen in 90° Bezüge.

Bild 7

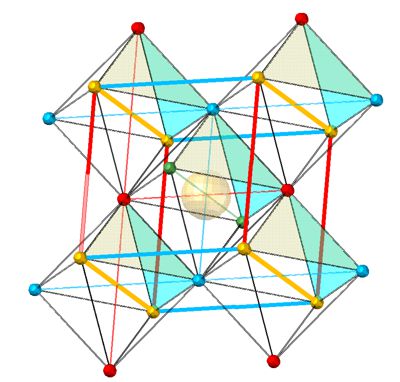
Die Diagonalen der Oktaeder jedoch hätten einen 90° x;y;z Bezug. Sie hätten jedoch eine Länge von λ·√2. So wäre eine Koordinatenangabe x; y; z möglich, jedoch hier nur bezogen auf das Zentrum des Oktaeders. Die Koordinatenwerte hätten so eine Quantelung von λ·√2. Um nun zu den einzelnen Punkten des so ermittelten Zentrums des Ziel-Oktaeders zu kommen, braucht es je nach gesuchtem Punkt zum Koordinatenwert lediglich +/-1x; +/-1y und +/-1z; dazu gezählt werden. In dem Sinne können alle Punkte eines 3D-Raumes von den Zentren der Oktaeder definiert werden. Es wäre ein Raum, dessen Markierung der Zwischenräume wieder den Tetraeder-Raum zeigen würde.

Bild 8

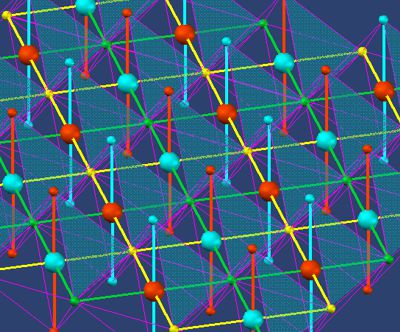
Sinn macht dieses Koordinatensystem nur, wenn es auch die 4. Dimension, die Zeit, definieren könnte. In Bild 8 wird sie als grosse farbige Kugeln dargestellt. Die 3D Koordinaten x; y als die Paritäten Gelb und Grün und z als die Paritäten Rot und Blau. Nur in so einer Einteilung erzeugen die Zentren der Oktaeder bei dem Kollaps der inneren Energie-Dichte die 4. Farbe (grosse Kugeln) als Indikator der 4. Dimension. Nur so kann sich die Einwirkung der 4. Dimension mit ausgeglichenen Paritäten (hier Blau und Rot) in unseren 3D-Raum vorgestellt werden.

Das Ergebnis: Es entstehen pro Zeitsequenz 2 Raumarten, einer aus Würfel mit blauen Kugeln (blauer Raum) und einer aus Würfel mit roten Kugeln (roter Raum). Diese beiden Räume sind um ½(λ·√2) versetzt. Der rote Raum steht (als Beispiel) für den 3D Raum in positiver Zeit und der blaue Raum steht für den 3D Raum in negativer Zeit. Als 4D Parität bedeutet das nur + / - und bedeutet das Äquilibrium des leeren Raumes. Wir leben daher in beiden Räumen, die Paritäten jedes unserer Atome wechselt in 4 Farben pro Zyklus, Spin (+/- in 3D) und Ladung (+/- in 4D) mit den Begriffen der Physik. Je nach Experiment werden diese Paritäten auch als Chiralität oder angular Momentum (Stern Gerlach Experiment) bezeichent.

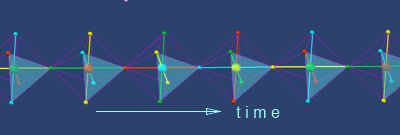Bild 9

Es ist ein echtes 4D-Koordinatensystem, welches Distanzen in einem starren Euklidischen Raum als gequantelte Werte angibt und wo die Parität der Schwingung am Zielort immer der Parität des Koordinaten-Nullpunktes gleicht. Anders wird es, wenn der relativistische Raum angenommen wird, wo die Distanz mit tc=√(x²-y²-z²-4d²) begrenzt wird. Je nach Distanz tc ergibt eine Energie-Mutation im Koordinaten-Nullpunkt eine Reaktionszeit von t={√(x²-y²-z²-4d²)}/c.
Da die Distanz mit λ gequantelt wird, theoretisch ein Zeitquant von λ/c, die Zeit, wo sich je nach Energiedichte (z.B. ein Proton-Feld) die Parität wechselt, ist der Farbwert am Ziel anders als der im Koordinaten-Nullpunkt.
Ist die Zahl der Quanten von (λ) = n, dann gilt z.B bei Farbe 1 = 1+(n-4·(integer n/4)) .
Ist es die Farbnummer 1, dann ist bei z.B. 41 Quanten-Längen die Parität 1+(41-4·10) = 2 .
Diese Art der Berechnung spiegelt die Zeitänderung wider, sie wird aus der Länge λ abgeleitet. Diese Rechnung müsste dann bei allen 4 Koordinaten im 4D-Raum gemacht werden.

Es ist ein Vorschlag für ein 4D-Koordinaten-System

Es ist wichtig zu beachten, dass alle Bilder außer Bild 9 eine Gleichzeitigkeit im Bild aufweisen. Es ist eine Eigenschaft unserer Fähigkeit, drei Dimensionen gleichzeitig zu sehen. Menschen der Zukunft könnten eventuell das Gleiche mit mehr Dimensionen sehen.

Da Wissenschaft und Physik das 4D-Verständnis vernachlässigt, hat sie neue Namen für jeden Effekt eines 4D-Volumen-Verständnisses gefunden. Der beobachtete Zyklus von Fermionen (4D-Objekten) hat daher ½ Spin, da es 4 Paritäten pro Zyklus (720°) hat und somit 360° nur 1/2 Zyklus ist. Heute wird das Bild rotierender Teilchen angezweifelt. Anstatt  die quantisierten angulare Momente sind es die 4 Spinoren Dirac’s. Ein Boson hat als 3D-Teilchen 2 Paritäten (360°), was als Spin 1 bezeichnet wird. Bosonen gehorchen der Schrödinger-Gleichung. Es ist klar, dass Bosonen keinen Zeitbegriff haben können. Sie werden damit zur Ausbreitung mit V=c gezwungen. Ohne Zeit wird die Mutation des Mediums im Quantum-Feld-Bezug gleichzeitig ausgeglichen.

Wir haben zwei Basis-Arten von Energieträgern gefunden; Protonen, Elektronen, Neutrinos als 4D-Volumeneffekt und alle Bosonen und Photonen als 3D-Ebeneneffekt. Anstelle des 4D-Volumeneffekts könnten wir den traditionellen Begriff „massetragendes Teilchen“ verwenden. Der Leser ahnt bereits, dass Masse nun erklärt werden soll.

Auf diese Weise kämen wir zum Higgs-Feld, einem Feld mit einer Qualität, um mit einem Higgs-Boson, einem Teilchen oder Feld mit einer so kleinen λ-Wellenlänge, zu interagieren, dass das Boson (sein Photon) eine unglaubliche Energie von 125 GeV hätte. Aber auch diese als Masse sind nur Spuren der 4. Dimension. Wir sollten daher die Teilchen-Physik anhand der oben beschriebenen 4D-MATRIX erklären.

Die beugungsrelativistische Raumzeit mit der Berücksichtigung des Lorentz-Faktors gehört nicht zu dieser Betrachtung. Wir verwenden hier einen starren 4D-Euklidischen Raum. Euklidisch deshalb, weil alle hier dargestellten Überlegungen auf einer Gleichzeitigkeit basieren, d.h. dass Zeit durch die Gleichzeitigkeit der 4D-Koordinate ersetzt wird. Wir wissen, dass diese Gleichzeitigkeit ein bestimmtes λ als Wellenlänge dieser Meßskala hat. Sie ist eine auf die Größe dieser Gleichzeitigkeit abgestimmte Schwingung mit der eine Wechselwirkung mit den zu untersuchenden Objekten erst möglich wird.

Ich möchte hier an den Einstein-Raum (Vortrag an der Universität Leiden 1919) erinnern. Es ist ein Raum, der keine Bewegung sondern nur Propagation zulässt. Das Medium steht still und ist starr, das Bewegte ist nur die Energie. Ein Proton existiert aus dieser Perspektive nicht, es ist nur die Energie, die im Zentrum des jeweiligen Oktaeders (Energiekollaps im Oktaeder) den Effekt eines Protons hat. Es ist nur diese Energie, die sich bewegt und nicht die Form des Protonenfeldes.

Die MATRIX Theorie ist ein 4D-Raum geometrischer Zuordnung von Punkten mit gleichen Abständen, das λ ihrer Schwingungen, die in 4 Paritäten oszillieren. Die MATRIX Theorie hat daher nur 2 Variable; Parität und Massstab.

Parität basiert auf den Energie-Schwingungs-Moment; das (+ -) der Elastizität des Raumes, dass Störungen mit V=c zur Normalität zurückbringt.

Massstab basiert auf das λ der Feldgrösse seiner Schwingung λ = h·c / E wobei h = Planck-Konstante = 4,135667...^-15 eV·s

Es ist klar, dass der Teilchen-Zoo der Physik nur mit diesen 2 Variablen erklärt werden muss!

Alle Geschehnisse sind das Ergebnis von Größe und Parität. Es gibt keine getrennten Dinge; Alles ist durch diese beiden Grundeigenschaften mit der MATRIX verknüpft.

Die Erklärung über Parität erfordert immer die Imbalance eines Mediums als (+) und (-).

Die Erklärung über Maßstab erfordert einen kleineren Maßstab als Medium des größeren.

Wechselwirkungen erfordern immer den gleichen Maßstab oder einen Maßstab mit einem ganzzahligen Verhältnis. Auf λ angewendet bedeutet das immer die gleiche Energie beider in Wechselwirkung stehenden Komponenten.

Komplexe Operationen reagieren immer zu der niedrigsten Energiebedingung. Dabei tendiert der Raum (<E = >λ) zur größeren Feldgröße was einer Entspannung des Raumes gleichkommt. Hiermit sind alle Aktionen miteinander verflochten; eine Abseitsstellung ist nicht möglich. Beobachter und Beobachtungen stehen auf derselben Seite.

Bild 10

Links; ein Kornkreis. Hier eine Interpretation:
Der große Kreis symbolisiert die Größe des gesamten Tetraeders. Die kleineren Kreise symbolisieren die Felder der Paritäten. Die Punkte in ihren Zentren zeigen die Felder mit Masse. Der kleine Kreis unten mit einem Mittelpunkt und weiteren Punkten nach unten symbolisiert das Medium des Mediums und so weiter. Hier werden die beiden Variablen Parität und Massstab dargestellt, das Bild zeigt die Theorie und ist als Information in dieser Weise perfekt.

Jemand da draußen scheint uns mehr über wahre Wissenschaft beibringen zu wollen, als wir in heutiger Zeit erfassen können. Unsere Physikergemeinde scheint jedoch noch nicht bereit zu sein, von ihrer alten 3D-Welt/Zeit zu einem 4D-Bild aufzusteigen.

Die 4D-Matrix ist jedoch nur eine vorläufige Betrachtungsweise. Mein Papier über die Sehweise des Universums im Kontext zur Matrix, siehe Matrix-universe, beschreibt nicht nur das Universum mit 4 Dimensionen, sondern seine Entstehung als Hotspot eines übergeordneten Zykluses in der 5. Dimension. Diese logische Anwendung geometrischer Dimensionen und ihrer Messweisen bezieht sich dort ausschließlich auf das Universum. Das Konzept von Dimensionen lässt sich logisch auch auf zusammenhängende Ereignisse wie das Schicksal von Lebenswegen im Kontext Zeit und Raum und Parallel-Welten anwenden. Im 21. Jahrhundert werden solche Konzepte sehr nützlich werden.

Künftige Generationen werden die Illusion «Raum» und Zeit» erkennen und gegen ein neues Bild multipler Dimensionen austauschen. Die Zeit wird zur 4D-Koordinate und mit der Zeit-Illusion wird der Raum ebenfalls zur Illusion. Ortswechsel passieren ohne Geschwindigkeit. Es ist nur ein Wechsel des Blickpunktes. Distanz und Zeit werden zur Hilfsgrösse ohne Wirklichkeit.

Für ein tieferes Verständnis zur Matrix-Theorie empfehle ich meine weiteren Schriften.

die Matrix des Weltmediums
Die Schwingung des Welt-Mediums
die Geometrie des Mediums Raum
Das Universum
Friedmann-space and the space-matrix
Das Raum-Zeit-Kontinuum
Die Raum-Zeit-Illusion
Das Elektron
Teilchen in der Matrix struktur

Gunter Michaelis, Griesbach den 27.12. 2023