Teil 3: Feldtheorie aus der Matrix des Mediums abgeleitet
In diesem Teil geht es um eine Quanten-Feld-Theorie, die sich zur Hauptsache von den Eigenschaften des Mediums, das Raum-Zeit-Pulse Kontinuum ableiten lässt. Die daraus entstandenen Phänomene wie Partikel, Masse/Trägheit, Ladung usw. werden hier erklärt.
Ein Partikel ist kein separates Feld, es ist der Zustand des Mediums an diesem Ort.
Aus diesem Blickwinkel entstehen in CERN keine neuen Partikel, es ändert sich nur der Zustand des Ortes. Alle Kräfte, alle Wechselwirkungen gehen aus den Störungen der ursprünglichen Oszillation des Raumes, der Zeit (auch sie oszilliert) und des entstehenden Pulses hervor. Anstatt Quantenzahlen werden die Zustandsformen des Ortes einbezogen. Dabei gibt es keine scharf definierten Orte mehr. Alles, was ist, ist Oszillation und hat in jeder Pica-Sekunde einen anderen Zustand. Nur die stetige Wiederholung, die zyklischen Muster sind das, was erkennbar ist. Dabei sind die kleinsten Zyklen das Medium der größeren. Es gibt kein Anfang, es gibt keine Planck-Länge oder abgeleitete Werte der Zeit und Masse.
Die messbare Physik hört nicht auf, wo die Messbarkeit aufhört.
Aber es macht auch keinen Sinn Grenzen zu suchen, wo keine sein können. Das Konzept einer Matrix als eine polydimensionale Geometrie erlaubt, die Geometrie der stehenden Felder zu erklären und ändert damit viele Standart-Interpretationen der Physik.
Trotz einer grundsätzlich starren Bestimmung der geometrischen Matrix muss mindestens eine Eigenschaft des Raumes erkannt werden. Der Grad der Freiheit verlangt eine Elastizität, ein Biege-Potential, das Verformung und Widerstand erlaubt. Erst diese Elastizität erschafft den Moment h=Pulse▪ʎ, eine Energieform E=hf (h=Planck-Konstande, λ=Wellenlänge, f=Frequenz). Da h invariabel ist, können sich in den Raumzellen nur λ und f ändern. Die Geometrie der Matrix verlangt jedoch, dass diese Änderungen in integer (ganzzahligen) Verhältnissen stehen. Für ein tieferes Verständnis siehe meine Schrift Feld und Quantum Dynamik)
 Hier
Blau ist energetisch gleich gross (S9) wie das rote verkleinerte Feld.
Hier
Blau ist energetisch gleich gross (S9) wie das rote verkleinerte Feld.
Die stehenden oder gebundenen Felder um das Zentrum eines Partikels haben eine eigene Metrik, d.h. eine relativistisch verzerrte Stabgröße, Puls und Frequenz. Eine Interaktion mit anderen Partikeln geschieht jedoch immer in der gleichen Metrik. So wechselwirkt ein Elektron mit einem Proton z.B. in S27 bis S81 (S=scale, wobei S1=Proton ist), dem Feld der Elementar-Ladung e=1,602·10-19 Coulomb des SM (Standard Modells), wie später im Teil 4 im Detail erklärt wird. Dort wird die Bezeichnung e=1eV=1240nm (Comton-λ) bevorzugt.
Das Standard SM verlangt bei der oben genannte Interaktion das
Kriterium der Ladung (+) oder (-). Diese wird von der MFT
(Matrix-Feld-Theorie) durch den Begriff Parität ersetzt, da MFT alle
Partikel als Oszillation auffasst, was ja ein Wechsel von (+) und (-)
bedeutet. Dieses aber erfordert die Aufgabe eines leeren Raumes
mit der Dynamic separater Teilchen. Ein Teilchen ist in
der MFT eine Modifikation des Raumes. Daher ist eine Teilchen-Oszillation
immer im gleichen Rhythmus wie sein Medium, hier der Ort x; y: z: t . Ein
Partikel ist daher in (+) Zeit nicht (+) sondern hat in diesem Ort x; y; z; t die
Parität (+). Egal
wo das Partikel der Interaktion (hier das Elektron) ist, es hat überall im
Raum das gleiche Paritäts-Verhältnis (nicht + oder - sondern nur das gleiche
Verhältnis zum Nachbar-Status.
Ein Proton hat an dem Ort der Interaktion immer die Gegenparität
des Elektrons.
Feld und Massstab
Der normale Begriff eines Feldes im Raum ist ein Bereich gleicher oder kohärenter Eigenschaften. Seine Form und Größe richten sich nach dem Maßstab seiner Wirkung (λ=h▪c/E). Das Medium verbindet Raum- und Zeit-Zellen zu einem Verbund gleicher Eigenschaften. In den kleinsten Maßstäben von Raum und Zeit, der Größenordnung von Protonen, Elektronen und Neutrinos werden Formen aus Oktaeder und Tetraeder gebildet.
 Im Maßstab der Ladungsfelder der
Elektronen (S9 bis S81) werden Felder der Elektronen zu bevorzugte Orte mit hoher
Treffer-Wahrscheinlichkeit (Elektronen-Nachweis). Im chemischen
Maßstab werden sie ziemlich rund. Dort verschwimmen die Quanten als Summe
vieler Quanten und werden als analoge Grössen wahrgenommen. Es sind multiple
Felder mit fast gleichen Zentren. Sie ergeben Mischgrößen, die aus
quantisierten Einzelgrößen (E=hF) und Gesamtgrößen mit einer
Verteilung E=multiples ΔE/r^2 bestehen. Aus den geometrischen Formen werden
in den --> Maßstab unserer Umgebung sphärische analogische Formen.
Im Maßstab der Ladungsfelder der
Elektronen (S9 bis S81) werden Felder der Elektronen zu bevorzugte Orte mit hoher
Treffer-Wahrscheinlichkeit (Elektronen-Nachweis). Im chemischen
Maßstab werden sie ziemlich rund. Dort verschwimmen die Quanten als Summe
vieler Quanten und werden als analoge Grössen wahrgenommen. Es sind multiple
Felder mit fast gleichen Zentren. Sie ergeben Mischgrößen, die aus
quantisierten Einzelgrößen (E=hF) und Gesamtgrößen mit einer
Verteilung E=multiples ΔE/r^2 bestehen. Aus den geometrischen Formen werden
in den --> Maßstab unserer Umgebung sphärische analogische Formen.
Dynamische und stehende Felder
 Aus
der Sicht der Raum-Zeit betrachtet hat ein Feld neben den Impuls ein Ort und
Zeit. Ein Photon ist daher ein propagierendes Feld, das den Ort mit V=c
ändert und die Zeit innerhalb seines Systems einfriert. Ein Partikel ist ein
Feld mit gleichem Ort aber messbarer Zeit. Die Sequenzen seiner Oszillation
bestehen aus dem Radius r bzw λ der Feldeschwingung und der Zeit=r/c.
Aus
der Sicht der Raum-Zeit betrachtet hat ein Feld neben den Impuls ein Ort und
Zeit. Ein Photon ist daher ein propagierendes Feld, das den Ort mit V=c
ändert und die Zeit innerhalb seines Systems einfriert. Ein Partikel ist ein
Feld mit gleichem Ort aber messbarer Zeit. Die Sequenzen seiner Oszillation
bestehen aus dem Radius r bzw λ der Feldeschwingung und der Zeit=r/c.
Ein Photon
verhält sich wie ein Teilchen, wenn es als Einzel-Impuls mit dem Zeitpfeil
Links und Rechts betrachtet wird. Es verhält sich wie eine Welle, wenn es
mit dem Parafeld (Überfeld) des Licht-Quants wechselwirkt bzw. interferiert.
Diese Parafelder können sehr gross sein und sind sinngemäss verflechtete
Wirkungen (Entanglement).
Im Prinzip wäre damit alles über Felder gesagt. In der Physik aber haben wir es vornehmlich mit der Wechselwirkung der Felder zu tun und diese erzeugt weitere Kombinationen. Kurz: Es gibt eine große Zahl von Feld-Varianten.
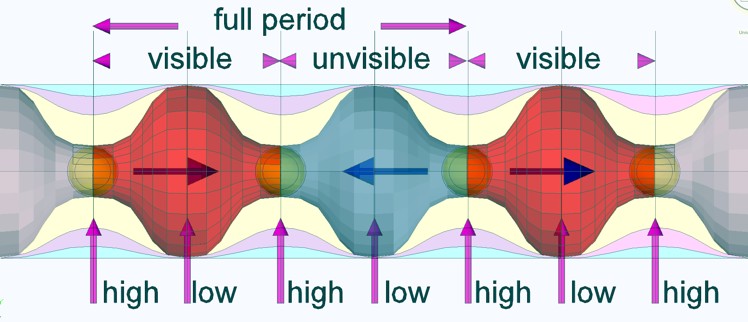
 Ein
Feld aus einem einmaligen multiplen Geschehnis mit radial auslaufenden
Wellen der Amplituden E=ΔE/r^2. Hier als Fläche dargestellt. Die z-Achse
zeigt hier die Energie der Amplitude.
Ein
Feld aus einem einmaligen multiplen Geschehnis mit radial auslaufenden
Wellen der Amplituden E=ΔE/r^2. Hier als Fläche dargestellt. Die z-Achse
zeigt hier die Energie der Amplitude.
X; Y; symbolisiert den Raum. Multiple
Ursachen erschaffen eher analoge Felder
Diese Betrachtung gilt nur für den flachen Raum. Da aber die Energien in den einzelnen Größen Bereiche (Skalen S1-Sx) komplett auseinander laufen, erschuf das SM in der Physik unabhängige Bereiche der Kräfte, die als Naturkräfte ohne tieferen Zusammenhalt hingestellt werden. Unten werden die Bereiche der starken und der schwachen Kernkraft sowie der EM-Kraft näher erklärt.
 Hier
ein stehendes Feld mit seinen Resonanz-Feldern. Der Oktaeder im Zentrum ist
das Primär-Feld. Im Falle eines Protons wäre seine Grösse S1 und im Falle
eines Elektrons S3. In dieser Größenordnung ist alles quantisiert. Eine
Wechselwirkung wäre nicht E=ΔE/r^2 wie bei multiplen Feldern sondern E=hc/λ,
wobei λ die Stablänge des Feldes wäre. Eine Wechselwirkung passiert hier nur
eindimensional. Die Stäbe in dieser Größenordnung symbolisieren die
„Strings“ der Wechselwirkung. Die Farben der dargestellten Punkte (Knoten
des Stoffes aus dem der Raum besteht) sind im Standart-Model der Physik die
Quanten-Chromo-Dynamik der virtuellen Teilchen. Ihre Oszillation ändert pro Quanten-Zeit ihre
Farben. Ihre Verhältnisse im Sinn eines Ausgleichs der Raumdichte jedoch
bleiben und werden Träger eines scheinbaren statischen Bildes. Im Status des ungestörten
Raumes gelten die Farben als Symbol ihres Zustandes (Pariität) der Oszillation.
Bei der Wechselwirkung
der „Felder“ werden Farben und Stablängen und somit auch Zeit und Energie
geändert. Jede Feld-Wechselwirkung ist das Spiel des Ausgleiches der
Raumdichte, physikalisch der Energie.
Hier
ein stehendes Feld mit seinen Resonanz-Feldern. Der Oktaeder im Zentrum ist
das Primär-Feld. Im Falle eines Protons wäre seine Grösse S1 und im Falle
eines Elektrons S3. In dieser Größenordnung ist alles quantisiert. Eine
Wechselwirkung wäre nicht E=ΔE/r^2 wie bei multiplen Feldern sondern E=hc/λ,
wobei λ die Stablänge des Feldes wäre. Eine Wechselwirkung passiert hier nur
eindimensional. Die Stäbe in dieser Größenordnung symbolisieren die
„Strings“ der Wechselwirkung. Die Farben der dargestellten Punkte (Knoten
des Stoffes aus dem der Raum besteht) sind im Standart-Model der Physik die
Quanten-Chromo-Dynamik der virtuellen Teilchen. Ihre Oszillation ändert pro Quanten-Zeit ihre
Farben. Ihre Verhältnisse im Sinn eines Ausgleichs der Raumdichte jedoch
bleiben und werden Träger eines scheinbaren statischen Bildes. Im Status des ungestörten
Raumes gelten die Farben als Symbol ihres Zustandes (Pariität) der Oszillation.
Bei der Wechselwirkung
der „Felder“ werden Farben und Stablängen und somit auch Zeit und Energie
geändert. Jede Feld-Wechselwirkung ist das Spiel des Ausgleiches der
Raumdichte, physikalisch der Energie.
Parität und Wechselwirkung
 Hier wird das Thema Parität oder Ladung des Teils 2 weiter vertieft
=>
Parität
Hier wird das Thema Parität oder Ladung des Teils 2 weiter vertieft
=>
Parität
Der Begriff Parität ist ein Begriff der Oszillation. Es fehlt noch ein
Teilaspekt der Matrix. Es ist der Hyperraum bzw. der 4D-Raum. Er ist erklärt
in der Haupt-Page
=>
Dimensionen . Er ist es, der in dem Medium, das eigentlich eine
elastische Impuls-Fortpflanzung von V=c hat, ein stehendes Feld erzeugt. Es
ist eine Oszillation senkrecht zum 3D-Raum. Nicht der Hyperraum selbst wird
hier behandelt sondern der Effekt, dass unser Raum in einer übergeordneten
Dimension eingebettet ist. Dadurch verliert der Raum als Medium seine letzte
klassische Eigenschaft des Euklidischen Raumes, er wird zum 4D-Raum. Die
"Zeit" ist ein menschliches Konzept der 4D-Koordinate und dient nur unserer
beschränkten Vorstellung. Das obige Bild zeigt einen 4D-Euklidischen Raum.
Die sich dort ergebene Doppel-Oszillaton ist hier der SPIN=1/2.
Der Raum selber kann verformt werden
Und er wird es. Und mit der Verformung ändert die Raum-Dichte und mit der
Dichte die Zeit. Die Zeit aber ist an den Raum gebunden, da sie ein Element
der Oszillation ist. Die Oszillation besteht aus dem Verbiegungs-Moment
Pulse • λ, und der Frequenz F.
λ = c/F ↔
Biegemoment = Pulse ▪ c/F (c/F = Wirkungslänge des Pulses).
Die Verformungs-Energie
erzeugt jedoch eine Gegenverformung, sodass es wieder zum Äquilibrium kommt.
Es gilt E-Verformung = E-Gegenverformung = Null
Damit wird die Stärke der transmittierten Kraft definiert und in Beziehung mit dem λ (Radius) der Raumzellen und deren Frequenz gesetzt. Je grösser die Kraft-Transmission, je kleiner die Raumzelle bzw. λ der Oszillation, die diese Raumzelle bildet. Alles wird dominiert von dem Moment h (Planck Konstante) des Mediums. Aus der absoluten Balance aller beteiligten Eigenschaften ergibt sich die Struktur der Matrix und aus ihrer Störung die Phänomene, die unsere Welt bilden. Auf diese Weise bestehen alle Existenzen aus derselben Raum-zeit, nichts ist getrennt.
Die Wechselwirkung der Zwiebelfelder
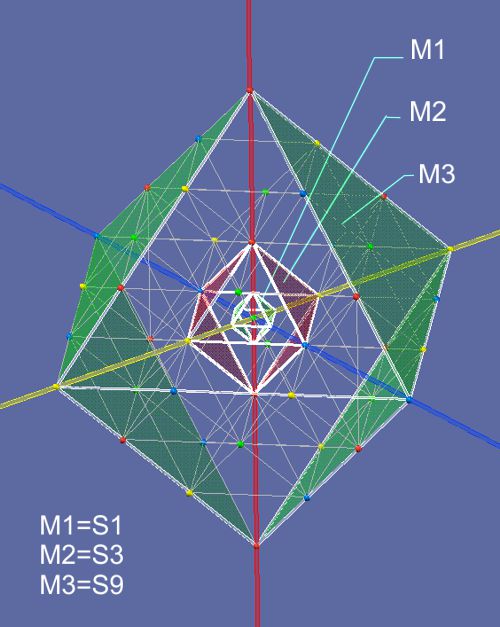 Ein
stehendes Feld kann aus geometrischer Sicht nur als Ursache eines Impacts
aus einer Dimension gesehen werden, die senkrecht zu den anderen Koordinaten
steht. Grundsätzlich gilt, dass es keine Begrenzung der Dimensionen
sondern nur eine Begrenzung unseres Verstehens gibt.
Ein
stehendes Feld kann aus geometrischer Sicht nur als Ursache eines Impacts
aus einer Dimension gesehen werden, die senkrecht zu den anderen Koordinaten
steht. Grundsätzlich gilt, dass es keine Begrenzung der Dimensionen
sondern nur eine Begrenzung unseres Verstehens gibt.
Siehe hier
Teil 1: Die Raumdimensionen
und Teil 2:
das neue Konzept der Zeit.
Unter diesem Aspekt entsteht mit dem Impact aus dem 4D-Raum ein Punkt-Feld,
das als Feld des Protons und als Massstab S1 für weitere Betrachtungen der
Raum-Geometrie benutzt wird.
Ausser dem Proton entstehen die
Primär-Felder der Elektronen und Neutrinos. Auf dem Weg zum Verständnis der
Partikel sind nur die Beziehungen der Protonen zu den Elektronen wichtig.
Die Neutrinos sind zu nah an der Energie-Fluktuation des Umgebungs-Raumes
bzw. an die pulsierende Entropie der Raum-Zeit. Sie haben keinen sichtlichen Einfluss auf die
Protonen- und Elektron-Wechselwirkung.
Bevor die unten gezeigten Bilder
erklärt werden, müssen Paradigmen neu definiert werden.
1.)
Ein stehendes Feld benötigt den Impact einer Ordinate aus dem 4D-Raum. Dieser ist eine
Oszillation, sie ist Energie, eine Tensor-Größe die senkrecht zu allen 3
Koordinaten des 3D-Raumes wirkt. Es fungiert als + und - zur Raumdichte und
initialisiert das lokale 3D-Feld.
2.)
Dieser Impact hat geometrisch keinen direkten Einfluss auf unsere Welt (der
3D-Raum). Dort sind alle Einflüsse indirekt. Das Primär-Feld des Impacts ist
daher eine im 3D-Raum indirekte und vom Impact nicht direkt ableitbare Größe. Die Formel E=mc^2
ist aus diesem Grunde nötig, da die formel E=h·c/λ reine 3D-Werte hat
und nur in wenig gekrümmten Raum gilt. In dem Sinne ist die
Energie E=h▪c/λ oder Puls▪λ▪c/λ hier das Ergebnis des Impacts und nicht der Impact selber.
3.) Der unter 2.) genannter theoretischer
Aspekt wird aber abgerundet mit der Annahme, dass der 3D-Raum von Schatten
höherer Dimensionen beeinflusst wird. So entsteht das Primär-Feld eines
Partikels zwar durch den 4D-Impact und seiner Amplitude E=hf, ist
aber keine direkte Ableitung, sondern ist das Resultat der Elastizität des
3D-Raumes.
4.) Die weiteren Felder um
das Primär-Feldes sind das Ergebnis des 3D-Raumes und werden hier als
Resonanz-Felder bezeichnet. Ihre Beziehung zu einander ist quantisiert d.h.
ΔE=hf/3. Der Faktor 3 kommt daher, weil auch Δλ = λ/3 gleich
dem Ratio der Zwiebelfeldgröße 3^x ist, d.h. das nächst größere
Resonanzfeld ist 3-mal größer (im oberen Bild S1 zu S3 usw.). Ein Partikel
präsentiert sich daher als ein Primär-Feld mit zwiebelförmig angeordneten
Resonanz-Felder. Diese sind es, die zwischen den Partikel in Wechselwirkung
treten. Nicht aber die Primär-Felder.
5.)
Alle Resonanz-Felder sind in den Maßstäben 3^x angesiedelt. Sie sind durch
Felder der Maßstäbe gerader Zahlen (S2; S4; S6; usw.) getrennt. Energien
können in den geraden Maßstäben (S2; S4; S6;) nicht gehalten werden und
verteilen diese mit V=c in das Umgebungsklima (Entropie). Ein Energiefeld ist daher
immer ein Feld im Maßstab einer
ungerader Zahl, wobei die größte Resonanz in den Maßstäben S3; S9; S27; S81 zu
finden ist.
6.) Alle Energien der
stehenden Felder im 3D-Raum sind Oszillation, ihre Durchmesser wurden daher als λ
bezeichnet. Siehe hierzu Oszillation
anstatt eines starren Raumes und Hyperraum
, bzw. Supersymmetrie
SUSI im Teil 2. Es gibt also zwei Schwingungen: eine wie bereits erwähnt aus
dem 4D-Raum und eine als Primärfeld im 3D-Raum. Daher wirken in jedem
Raumteil (das Medium der Raumes) 4 Paritäten (++) (+-) (-+) (- -).
7.) In der Betrachtung der Physik werden die Energie-Zustände
(Paritäten) der Zeit nicht benutzt. Das
Proton bekommt daher die Parität (+), das heißt, dass willkürlich nur
dieser Teil (+) der Oszillation betrachtet wird. Ein Elektron hat in
dieser Betrachtung immer die Parität (-). Richtiger wäre zu sagen,
das Elektron hat immer, wo es auf ein Proton trifft, die Gegenparität.
8.) Entsprechend der Erklärung der
Partikel als Oszillation, siehe
Ladung/Parität
, ziehen sich
stehende Felder grundsätzlich immer an. Das wird dadurch erklärt, dass
Oszillationen immer eine Tensor-Größe sind, die senkrecht auf die Vektoren
des 3D-Raumes stehen. Die Vektoren im 3D-Raum heben
sich im Gesamten mehr oder weniger auf. Die Tensoren aus dem 4D-Raum jedoch
haben nur eine Richtung (Oben-Unten) und können sich nur addieren (Gravitation). Ihre
Zentren nähern sich an bis die
Amplituden ihrer Sekundär Felder zu steil werden. Dies kann erklärt werden wie ein Bergsteiger,
der nach jedem Berg in ein noch tieferes Tal steigen, um dann einen noch
steileren Berg erklimmen muss. Irgendwann fehlen ihm die Kräfte und er fällt
zurück in das letzte Tal. Bei der Wechselwirkung der Partikel durchdringen
sich ihre äußeren Felder bis dahin, wo die Amplituden zu steil werden.
In den nachfolgenden Diagrammen wurde die Null-Linie am Boden gezeichnet, das heißt (+) hat die Farbe Rot und (-) hat anstatt unter der Null-Linie die Farbe Blau. So konnte das Beispiel Berg und Tal besser dargestellt werden. Es sind jedoch immer Oszillationen d.h. Blau und Rot wechseln mit der Frequenz (c/λ).
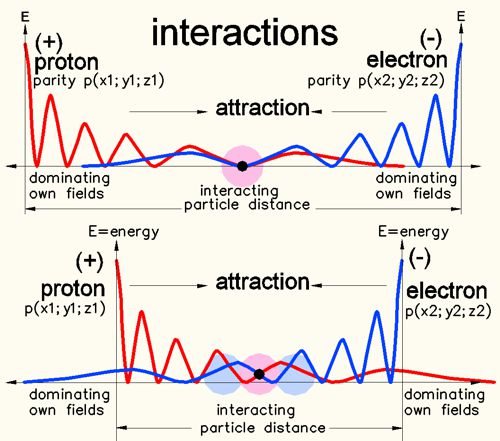 Oben: Es wird der Teil der Resonanz-Felder, die als Ladungs-Feld bezeichnet
werden, ineinander geschoben. Blau wird dem Elektron und Rot dem Proton Proton
zugeordnet. Das Ladungsfeld
hat kleine zentrisch angeordnete Subfelder, die hier als Felder mit immer
kleiner werdender Amplitude dargestellt wurden.
Da Blau und Rot am gleichen Ort sich aufheben, wird der Raum abgeflacht, es
entsteht Attraktion.
Oben: Es wird der Teil der Resonanz-Felder, die als Ladungs-Feld bezeichnet
werden, ineinander geschoben. Blau wird dem Elektron und Rot dem Proton Proton
zugeordnet. Das Ladungsfeld
hat kleine zentrisch angeordnete Subfelder, die hier als Felder mit immer
kleiner werdender Amplitude dargestellt wurden.
Da Blau und Rot am gleichen Ort sich aufheben, wird der Raum abgeflacht, es
entsteht Attraktion.
Unten: Das gleiche Szenario jedoch mit kleinerem Abstand der Partikel. Der
Abstand der Zentren ist abhängig von der lokalen Entropie, d.h. Dichte des
umgebenden Raumes.
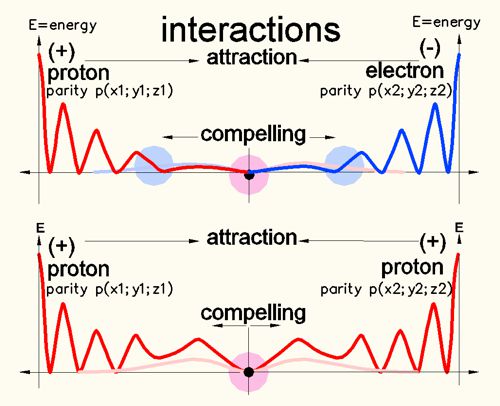 Oben:
Wechselwirkung eines Protons mit einem Elektron. Die Interferenz der
Gegen-Paritäten erschafft einen größeren Bereich der Raum-Glättung als mit
gleicher Parität.
Oben:
Wechselwirkung eines Protons mit einem Elektron. Die Interferenz der
Gegen-Paritäten erschafft einen größeren Bereich der Raum-Glättung als mit
gleicher Parität.Unten: Auch Felder gleicher Parität ziehen sich an. Das Energieniveau des abstoßenden Bereichs ist jedoch wesentlich höher. Im Falle bei Protonen wäre es das Energieniveau im Inneren des Atomkerns.
Das Standardmodel (SM) erlaubt nur der Elektromagnetik die +/- Attraktion, der Gravitation jedoch nur Attraktion. Da im subatomaren Bereich nicht nur +/- sondern auch ++ usw. Paritäten der Anziehung unterliegen, erfand man die Gluonen als Ersatztheorie. Da spielt jedoch auch die Einstellung, dass Raum prinzipiell leer und ohne Medium gesehen wird, eine Rolle. Solche theoretischen Verzirrungen werden in der Matrix-Theorie nicht zugelassen. Es gilt eine Raumverdichtung wo immer Masse ist. Sie wird durch die Oszillation senkrecht zum Raum erzeugt (in Richtung Zentrum der 4D-Sphäre). Diese allgemeine Anziehung der Teilchen wird jedoch von den Sekundär-Feldern, die sich um jedes Teilchen anordnen, abgeblockt (Pauli Exklusion). Die Überwindung dieser Felder benötigt riesige Kräfte, die normalerweise in den galaktischen Zentren angenommen werden (Kernfusion). Die Protonen im Kern liegen somit in einem tiefen Tal der Überschneidung ihrer Nachbar-Sekundärfelder. Sie haben dort einen stabilen Standort und brauchen keine Extra-Partikel.
Zum tieferen Verständnis:
Die Partikelfelder sind
"stehende" Felder bestehend aus dem Primär-Feld und den zentrisch angeordneten
Sekundär-Feldern. Die Interaktion in den Feldgrößen S9 – S27 wird hier als
Elektronenbindung der Ladungsfelder im EM-Raumes gesehen. Alle Interaktionen stehender Felder basieren
in der Matrix-Theorie auf der Annahme,
dass die Struktur des Raumes (sein Netzwerk) durch
Oszillationen
mit Tensor in Richtung 4D zusammengezogen wird. Da alle Partikel Oszillationen sind, entsteht
allgemein eine Verdichtung des Raumes, eine Entropie der Raumdichte, die somit größer als die Null-Dichte des
leeren Raumes ist. Die
Entropie des Raumes erlaubt
bei einer Aufhebung der oszillierenden Schwingungen (Interferenz bzw. (+) und (-) Kombination) eine Glättung des Raumes,
was den umgekehrten Effekt der Verdichtung bewirkt. Aus diesen beiden
Raumzuständen entsteht die Anziehung und Abstoßung. Anziehung ist daher
die Glättung des Raumes (+ / - = Anziehung) und Abstoßung die Verdichtung
des Raumes (+ / + oder - / -) bei gleicher Entropie. Diese Raum-Konditionen ersetzen damit
den Begriff "Ladung", der eine willkürliche Interpretation ist.
Die Grundkräfte der Physik
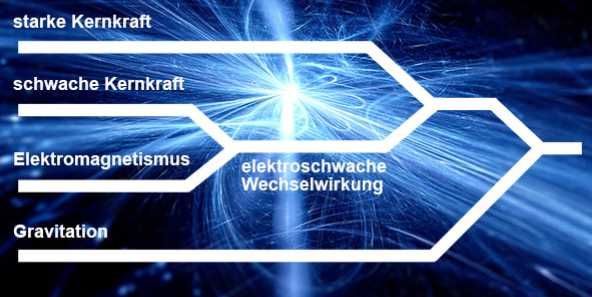 Ein
Bild vom Wissenschaftsmagazin Scinexx
Ein
Bild vom Wissenschaftsmagazin Scinexx
Die Matrix bietet eine Erklärung dafür, dass sich alle Grundkräfte der
Physik direkt aus dem Maßstab der räumlichen Struktur ableiten lassen.
Grundsätzlich gilt auch hier
λ=h▪c/E
oder λ=h/c▪m
(λ = Stablänge)
In
SM (Standart Model) würde es nur für die
EM-Kraft gelten. Aber der Raum ändert seine grundlegenden Eigenschaften
nicht, er ist in jedem Kraftbereich der wohlbeschriebene EM-Raum, dessen
Felder im Bereich starker Kernkräfte mit ihren steilen Amplituden (Pauli
Exclusion) die
Wechselwirkungen einschliesst. Der
Einfluss der relativistischen Metrik wird relevanter, je kleiner der Maßstab
ist. Sie ist abhängig von der Matrixstablänge "λ". Obwohl als Kraft
bezeichnet, entsprechen diese Wechselwirkungen nicht dem üblichen Bild des
Begriffs „Kraft“. Sie sind immer eine Schwingung. Es gibt im Grunde 2
Kontrapunkte, die immer einen Abstand haben. Die Entfernung in solchen
kleinen Maßstab ist jedoch eine Eichinvarianz. Auch die Abstandsänderung ist immer
eine Schwingungsperiode, d.h. sie hat Länge und Frequenz, die dem Raum
entsprechen müssen, in dem dieser Vorgang stattfindet. Je nach Anordnung der
subatomaren Forschungsansätze und indirekten Messmethoden (Eichtheorie)
haben raumverformende Energien die unterschiedlichsten Größen. Da die
Quantendynamik nur diskrete Werte zulässt, wurden diese Werte der
Feldverformung in SM als separate Teilchen gesehen. Die Matrix
Theorie aber
sieht diese Bosonen (Glouons, W- und Z-Bosonen) als gefangene Photonen im
Feld-Bereich der
starken Kern-Kraft.
Die starke Kernkraft ist für die
Chromodynamik der Quarks im SM (Standardmodell) verantwortlich.
Es sind Quanten in S1. Die Matrix-Geometrie und die
Dynamik der Planck Konstante lassen in der Matrix-Theorie ein
vollkommen anderes Bild entstehen. Anstatt Quarks werden die
Austauschteilchen zu Bosonen, im Princip Photonen mit 4D-Tensor in S1. Erst
ab S9 können Austauschteilchen als Photonen wahrgenommen werden.
Die Oszillationen des Kern-Feldes S1 erschafft mit Amplitude / Gegen-Amplitude
ein Feld, das von einem hohen Pauli-Exclusion-Feld umgeben sind.
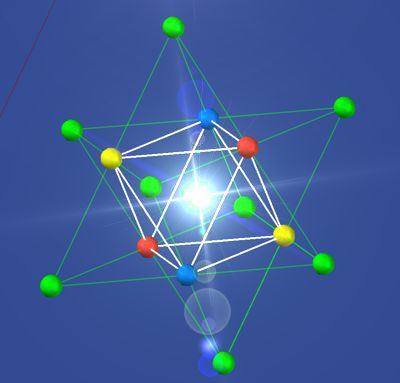 Hier kurz: Die Matrix sieht
den Ursprung dieser Kraft als Impulse aus dem 4D-Raum im Zentrum
des Teilchens (Oktaeders). Die 3 Diagonalen des Oktaeders bilden in ihren Richtungen eine
Kette gleicher Farben. In diesem Sinne sind sie wie Energieautobahnen. Sie
werden vom SM als Quarks betrachtet. Die Matrixtheorie
sieht sie als Lichtblitze mit einer Lebensdauer von etwa 1o^(-25) Sekunden
und nicht als Teilchen. Es ist die Interaktion innerhalb von S1, die nur bei
einer Kernzerstörung im LHC (z. B. CERN in Genf) auftritt. Bei näherer Betrachtung
des Protonen-Zusammenstoßes im LHC drückt die kinetische Energie das Proton
tief in die 4D-Ordinate des 4D-Raums. Die Wiederherstellung des alten
Zustandes geht durch verschiedene Ebenen der Raummatrix. Die freigesetzten
diskreten Energiestöße entlang der 3 Diagonalen des Oktaeders werden dann als
3 Quarks bezeichnet. Diese ergeben nur zusammen mit dem Proton selber ein
Äquilibrium. Ladung = p++; Quarks = up+-; down- -; up-+ .
Siehe hier zu auch
Ladung
Hier kurz: Die Matrix sieht
den Ursprung dieser Kraft als Impulse aus dem 4D-Raum im Zentrum
des Teilchens (Oktaeders). Die 3 Diagonalen des Oktaeders bilden in ihren Richtungen eine
Kette gleicher Farben. In diesem Sinne sind sie wie Energieautobahnen. Sie
werden vom SM als Quarks betrachtet. Die Matrixtheorie
sieht sie als Lichtblitze mit einer Lebensdauer von etwa 1o^(-25) Sekunden
und nicht als Teilchen. Es ist die Interaktion innerhalb von S1, die nur bei
einer Kernzerstörung im LHC (z. B. CERN in Genf) auftritt. Bei näherer Betrachtung
des Protonen-Zusammenstoßes im LHC drückt die kinetische Energie das Proton
tief in die 4D-Ordinate des 4D-Raums. Die Wiederherstellung des alten
Zustandes geht durch verschiedene Ebenen der Raummatrix. Die freigesetzten
diskreten Energiestöße entlang der 3 Diagonalen des Oktaeders werden dann als
3 Quarks bezeichnet. Diese ergeben nur zusammen mit dem Proton selber ein
Äquilibrium. Ladung = p++; Quarks = up+-; down- -; up-+ .
Siehe hier zu auch
Ladung
Die schwache Kern-Kraft ist im Bereich von S1 bis S3 (Pauli-Feld), aber auch im Bereich S5 bis S9
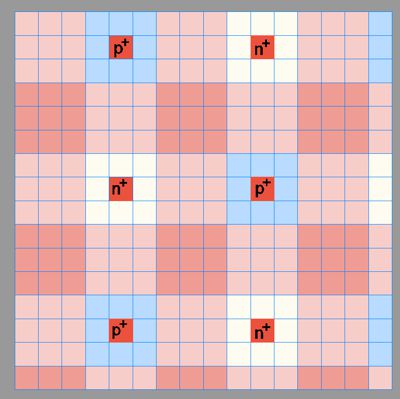 im Neutrino-Bereich
(Beta-Zerfall). Wir können hier
mehrere Abweichungen vom SM erkennen. Diese hängen jedoch
hauptsächlich von der Interpretation ab. Die Matrix hat den Vorteil einer
festen räumlichen Struktur, die insbesondere im Bereich der Quantendynamik
zur Orientierung genutzt werden kann. Die meisten Änderungen in diesem
Bereich sind in S5, S7 und S9. Die dortigen Wechselwirkungen ergeben eine
völlig neue Sicht auf Neutrinos. In Teil 4 wird es genauer erklärt. Das Bild
zeigt hier Protonen (P+) und Neutronen (n+-). In der Skala S1 hat ein
Neutron die gleiche Parität wie ein Proton (hier rot). In S3 ist es aber
neutral (weiß). Die Interaktion findet in S9 statt. Die Eichinvarianz führt
zu einer dominierenden
Raumabflachung, was hier eine Anziehung bedeutet. Selbst Spitzen und
Täler in dieser Skala sind unvorstellbar hoch (EM-Raum), die Eichinvarianz
(Elastizität) ist sehr schwach.
im Neutrino-Bereich
(Beta-Zerfall). Wir können hier
mehrere Abweichungen vom SM erkennen. Diese hängen jedoch
hauptsächlich von der Interpretation ab. Die Matrix hat den Vorteil einer
festen räumlichen Struktur, die insbesondere im Bereich der Quantendynamik
zur Orientierung genutzt werden kann. Die meisten Änderungen in diesem
Bereich sind in S5, S7 und S9. Die dortigen Wechselwirkungen ergeben eine
völlig neue Sicht auf Neutrinos. In Teil 4 wird es genauer erklärt. Das Bild
zeigt hier Protonen (P+) und Neutronen (n+-). In der Skala S1 hat ein
Neutron die gleiche Parität wie ein Proton (hier rot). In S3 ist es aber
neutral (weiß). Die Interaktion findet in S9 statt. Die Eichinvarianz führt
zu einer dominierenden
Raumabflachung, was hier eine Anziehung bedeutet. Selbst Spitzen und
Täler in dieser Skala sind unvorstellbar hoch (EM-Raum), die Eichinvarianz
(Elastizität) ist sehr schwach.
Der elektromagnetische Bereich (EM-Feld) ist in der Matrixtheorie
grundsätzlich
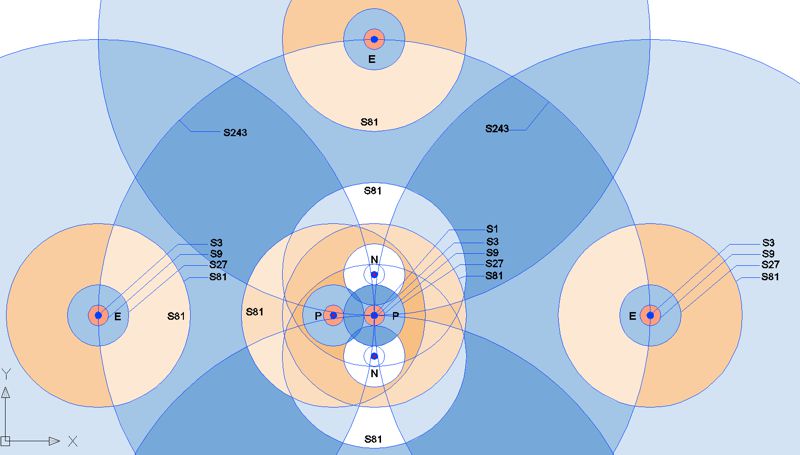 im
ganzen Raum
und allen Maßstäben. Im SM beginnt es in S9, dem nächst
schwächeren Feldbereich nach dem der Neutrinos. S9 - S81 ist der Feldbereich
(Maßstab) der Elektronen-Bindungen, der Wechselwirkung
zwischen Protonen und Elektronen, die gleiches Energieniveau haben
müssen. Aus diesem Grund interagieren sie in der gleichen Größenordnung (der
Elementar-Ladung S27 ~ 1eV). Die
Energiequanten sind dort Photonen. Aus Sicht des Matrixraums ist das
Energieniveau des Wechselwirkungs-Feldes (z.B. S27) für Elektronen und Protonen
immer gleich, hat aber immer die
entgegengesetzte Parität.
im
ganzen Raum
und allen Maßstäben. Im SM beginnt es in S9, dem nächst
schwächeren Feldbereich nach dem der Neutrinos. S9 - S81 ist der Feldbereich
(Maßstab) der Elektronen-Bindungen, der Wechselwirkung
zwischen Protonen und Elektronen, die gleiches Energieniveau haben
müssen. Aus diesem Grund interagieren sie in der gleichen Größenordnung (der
Elementar-Ladung S27 ~ 1eV). Die
Energiequanten sind dort Photonen. Aus Sicht des Matrixraums ist das
Energieniveau des Wechselwirkungs-Feldes (z.B. S27) für Elektronen und Protonen
immer gleich, hat aber immer die
entgegengesetzte Parität.
Die Matrix sieht den Bereich S81 - S243 für
die chemischen Bindungen von Feststoffen. S244 bis S=729 steht für
flüssige und S=730 bis S=2187 für gasförmige Materie. Weitere warten auf
ihre Entdeckung
Welche Rolle spielt die Planck-Konstante h in der Matrix
Was ist eigentlich h? h=E/f, es ist die Pulse-Energie einer
Schwingungs-Sequenz der Frequenz f.
Weil h invariant ist, sind E und f proportional kohärent. h
wäre hier der Impact, kompatible zu den Einheiten der Energie.
h = E/f ↔ (m▪c^2) ▪ λ/c , ↔ m▪c▪λ.
h = m▪c▪λ ↔ Pulse multipliziert mit seiner Aktionslänge.
h ist das universale Quant. Es ist Pulse ▪ λ.
h ist der Moment des
Pulses multipliziert mit der Wellenlenge ↔ p▪λ , wo λ die Distanz ist, die
die Aktion einer Sequenz mit V=c zurück legt. Dieser Moment ist eine Konstante
an der Basis unserer physikalischen Welt. Dieses p▪λ ist der Basis Moment
h. Theoretisch ergibt dies 2 Grenzwerte:
1.) m
= unendlich und λ = Null
2.) m = Null und λ = unendlich
(daraus ergibt sich,
dass unser Universum endlich begrenzt sein muss).
Grenzwert 1: Aus der Sicht der Matrix hat der Wert λ
der subatomaren Kraft in S1 (Maßstab des Protons) hier ~
1.3▪10^(-15) m und eine Ruhe Masse von ~ 938 MeV.
Grenzwert 2: Er ist wahrscheinlich viel kleiner als
angenommen. Er liegt in der Größenordnung, wo ein Quanten-Effekt nicht mehr
nachweisbar wird. Von da an hat der Quanteneffekt h=mc▪λ keine
sichtbare Wirkung. Die Energie E=hf wird zur Verdünnungsformel
(Kraftausbreitung) 1/λ^2
Die Planck Konstante ist 6,63 10^(-34) J▪s, ein Wert, den niemand, auch nicht Planck selber sich vorstellen kann. Es ist der Impakt eines Photons von der Grösse von λ=300'000 Km. Wenn man bedenkt, dass ein Photon von 1 Nanometer nm nur eine schwach wärmende Wirkung hat, dann hat ein Photon von ca. 1 Meter keine Wirkung mehr.
Ich benutzte daher anstatt des Riesen-Photons λ=300'000 Km von Planck ein Photon von λ=1 nm als Referenz, was dann eine Wirkung von 1240 eV hätte. Das kann ich mir so gerade noch vorstellen. Unter diesem Aspekt wären die Elektronen um den Atomkern im Grössenbereich von S81 = 1240 nm, da ja dort die Elementar-Ladung = 1eV zu finden wäre. Das wäre eine kleine Vorstellunghilfe. Die Wechselwirkung eines H-Atoms zum Einzel-Elektron von 13.4 eV hätte dann die Grösse von λ~1240/13.4=92 nm. Das wäre die kleinste Distanz des Elektronen-Ortes.
Man könnte sich eine vibrierende Konstruktion vorstellen, die beim Zusammendrücken schneller vibriert (der Abstand von V=c wäre kleiner und die Anzahl der Rückschläge größer). Umgekehrt wäre ein Impuls im kosmischen Maßstab (wie ein riesiges sternengrosses Photon) für sich allein und irgendwann wäre ein Rückschlag nicht mehr möglich. In diesem Punkt wäre die Energieverteilung E=∆E/λ^2. Der Aufprall hätte dann unabhängig von λ, der Entfernung von der Quelle, immer die gleiche Größe. Es gilt nur eine Verteilung (E=1/r^2).
Wir sind in der Größenordnung der Gravitation
Und hier finden wir die schwächste Kraft, die Gravitation, die letzte vom Standard Modell erkannte Grundkraft der Physik. Die Matrix-Theorie unterstellt der Gravitation die gleichen Gesetze wie die der subatomaren Felder. Allerdings gibt es einen grundsätzlichen Unterschied: Das Gravitationsfeld ist nur Phänomen des 3D-Raumes, die Ursache kommt aus der 4. Dimension. Die Präsenz der 4. Raum-Dimension wird in der Schrift MATRIX1 Dimension aufgezeigt. Um es klar zu stellen; unser Universum ist poly-dimensional, wovon mindestens 4 Dimensionen benötigt werden, um das Standard Modell zu erklären. Das Verschweigen der 4. Dimension in der Physik erschafft etliche Paradoxe und unerklärte Phänomene. Die Matrix-Theorie sieht den Raum und seine Felder 4 dimensional. Die Zeit ist der Schatten der D4-Dimension. Leider arbeitet die GFT (Allgemeine Feldtheorie) nur mit 3 räumlichen Dimensionen und trennt die Zeit.
Hier nun
die Erklärung, warum c auch in n Dimensionen immer gleich bleibt, auch wenn
ein n-dimensionaler
Freiheitsbereich mathematisch gesehen die Dimensionen D1; D2; D3 deutlich reduzieren würde. V=c wirkt
nur in Richtung V (Bewegungs-Richtung). Die Definition von d=V▪t ist immer eindimensional. Die
anderen Dimensionen definieren zwar den Anfang- und Endpunkt, haben
quantiativ keinen Einfluss auf V. Das gilt für V=c. Wie wir in unserer kosmologischen Betrachtung
MATRIX1 die Natur der Matrix zuvor gesehen
haben, dehnt sich unser Universum mit V=c radial vom Anfangszentrum
(Urknall) aus. Dies ist die gleiche Situation, als würden wir mit V=c reisen.
Alle anderen Koordinaten D1; D2; D3 werden nicht durch die
4D-Relativität beeinflusst, weil sie senkrecht zur D4-Koordinate
sind.
Es besteht keine Notwendigkeit, im 3D-Raum V=c auf V=c√2 zu erhöhen. Der Hyperraum jedoch
ist 4 dimensional und dort ist seine Relativität im 4D-Raum
ct=√(d1^2+d2^2+d3^2+d4^2),
wobei d1=die Distanz in D1, d2 in D2 usw ist.
Das bedeutet nicht, dass die Koordinaten in 4D
V=c wären. Somit ist max. c
in Bewegungsrichtung in allen Dimensionen
c.
Um das Bild klarer
zu sehen, wir haben nicht die Freiheit von 4 Koordinaten, wie es auf den
ersten Blick scheint. Die 4. Dimension ist voll mit ihrer Hyperdynamik
beschäftigt und somit nicht mehr im Spiel der Raumdynamik. Auf diese Weise ist
Einsteins Gleichung
max V3D=<ct=√(d1^2+d2^2+d3^2) in menschlichen Maßstäben immer
noch korrekt.
Nun, wie entsteht ein Gravitations-Feld? Nur „stehende“ Felder können ein multiples Feld erzeugen. Sie haben eine Ruhe-Masse in ihrem Zentrum, die wiederum die Sekundär-Felder zwiebelförmig um das zentrale Primär-Feld entstehen lassen. Wie im Kapitel Zwiebelfelder gezeigt wurde, erzeugt die Oszillation in Richtung der 4. Dimension eine Verkleinerung aller Masse-Felder. Ein Feld kann viele Arten von Energie tragen, die alle eine Vektor-Größe bilden. Es sind Impulse mit einer Richtung. Eine Art von Impuls hat jedoch im 3D-Raum eine Tensor-Größe (keine Vektor-Größe). Das ist so zu verstehen, dass die Größe des Impulses selber oszilliert, was eine Vibration der Feldstärke nach innen gleich kommt. Während in einem multiplen Feld (Feld-Haufen) sich alle Vektoren mehr oder weniger aufheben, können sich Tensor-Größen der 4. Dimension nur addieren. Das Ergebnis in einem multiplen Feld (z.B. Planet Erde) ist eine signifikante Erhöhung der Attraktion, allgemein als Gravitation bekannt. Im oder in unmittelbarer Nähe dieses Multiplen Feldes kann die klassische Verteilung der Attraktion radial nach außen mit F/r2 (Kraft/Radius^2) gesehen werden. Hier sind die Feld-Zentren im Verhältnis ihrer Standorte zu ihren schwachen Wirkungen soweit verteilt, dass eine Fokussierung aller Felder als eine Quantenstruktur nicht erkennbar wird und verschwimmt. So ein Feld attracts in allen Richtungen, außer in Richtung 4D, wo es als Zeit gesehen wird.
Anders sieht es jedoch in einer Entfernung von etwa 1 Lichtjahr aus. Dort
wird die Feldwolke (hier z. B. die Erde) zu einem scharf umrissenen Punkt in
Bezug auf die riesige Entfernung von 1 Lichtjahr. Die Unschärfe der
Quellorte wirkt sich hier nicht mehr aus. Es werden wieder Feldstrukturen der
4D Tensoren (und
nicht der sich selber störenden Vektoren) erkennbar. Es bildet sich die „Oort-Wolke“.
In weiteren kosmischen Distanzen können sich immer klarere Strukturen wie
die Quantenstruktur der Atom-Maßstäbe etablieren. So werden Interferenzen
und Kulminationen kosmischer Felder großer Distanzen (mit λ von vielen
Lichtjahren) so manche heute unerklärbaren Phänomene erklären.
Der Raum
ist durch seinen Quanteneffekt stärker gekrümmt als von der Wissenschaft
angenommen. Es kann nicht durch die Verteilung von 1/r^2 erklärt werden. Der
Raum hat in kosmischen Distanzen die gleiche Verteilung wie Felder im
atomaren Kleinmaßstab. Hier ein Beispiel: Perlenketten
von Sternen von bloßen Auge erkennbar wären ein guter Beweis.
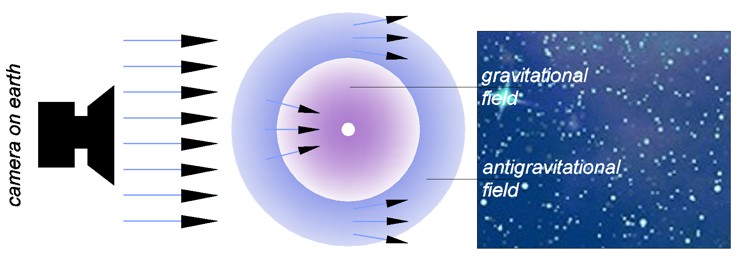
Die Weltstrings
Wie oben beschrieben, kommt die Pingpong Kraft
h=mc▪λ kaum noch zur Wirkung, da der Weg des
Impulses bzw. Pulses mit V=c zu lang und die Frequenz zu Größen unter 1
wird. Da die Distanz aus der quantendynamischen Formel wegfällt, wird aus E=hF ↔
E=h. Hier wird es als
Pulse bezeichnet. Der Puls erschafft im Quanten-Maßstab das stehende Feld.
Dieses erzeugt, wie in den vorgängigen Artikel beschrieben, die
Resonanz-Felder als sekundärer Effekt des 3D-Raumes. Diese werden aus
Gründen geometrischer Harmonie im Ratio von 3^x zum nächsten Feld immer
grösser.
Der moderate Puls wird daher immer kleiner. Der moderate Puls ist
eigentlich die multiple Puls-Wirkung pro Zeiteinheit. Die Zeit ergibt sich
aus c/λ, d.h. je grösser λ, je grösser der Zeit-Abstand zwischen den
Einzelpulsen und damit je kleiner die Anzahl der Impacts. In dem Sinn wird
der moderate Puls schwächer. Im Sinne der analogen Physik wird dann die
Distanz größer. Aber schon im Maßstab der Quanten Theorie sind die
sphärischen Felder nur Wahrscheinlichkeiten. Der Physiker spricht vom
Kollaps der Wellen-Funktion bei einer Wechselwirkung. Da Wahrscheinlichkeit
keine physische Realität besitzt, ist der Puls vom Anfang an nur ein String,
der aber wegen seiner hohen Oszillation als ein statisches Gebilde gesehen
wird. In der Quanten-Theorie ist die Vorstellung von sphärischen Feldern
sinnvoll, da diese aus immer gleichen Feldabständen die Geometrie der Matrix
ergeben. In größeren Maßstäben wird es sinnvoll, den Puls und auch den
moderaten Puls als String zu sehen. Als String jedoch fällt die Abhängigkeit
von Frequenz F und der Schwingungswelle λ weg, es gilt nur die
2-dimensionale Energie-Verdünnung 1/r^2. Es ist wie beim See-Igel: Je näher
zum Körper des See-Igels, je dichter die Stacheln. Im See-Igel Körper finden
wir anstelle der Stacheln (Einzel-Puls) nur den moderaten Puls. Im Bereich
der Stacheln befinden wir uns im Bereich der Weltstrings. Sie wirken im
Messbereich unserer Instrumente zwar immer noch als ein moderaten String,
haben jedoch schon die Verteilart der Gravitation bzw. E=1/r^2.
Die Gravitationskraft wäre dann F=G•m/r2. Für die Theoretiker: Die Quantentheorie wäre dann nicht verletzt. Die Feldtheorie ebenfalls nicht. Der Wellenkollaps wäre mit der ein-dimensionalen Formel E=hF erklärt. Somit hat die String Theorie ebenfalls ihre Erklärung. Bei der Matrix-Theorie sind Wechselwirkungen ebenfalls nur 1-dimensional möglich.
Matrix und die Illusion der Teilchen

Die Matrix erklärt den leeren Raum als Medium aller physikalischen Dinge. Die Matrix als eine geometrische Struktur eines Raumes von Tetraeder und Oktaeder wird aus unserer Sicht als Nichts gesehen, da ihre Elemente, die Tetraeder, in sich ein Equilibrium all ihrer Eigenschaften sind. Die Summe seiner Momente ist Null. Die Matrix wird unsichtbar. Die Störungen dieses Equilibriums in Form als Oszillationen ergeben die Dinge, die unsere Welt ausmachen.
Normale Störungen bzw. Momente propagieren mit V=c durch die Matrix-Struktur unseres 3D-Raumes. Es sind Vektor-Momente, Oszillationen, die mit jeder Parität ihrer Oszillation den Ort ändern. Wird die Matrix-Struktur nicht erkannt, so werden diese Störungen als Teilchen gesehen. Die Physik spricht deshalb von Photonen oder Bosonen anstatt von oszillierenden Momenten.
Werden Störungen durch Druck, Dichte und Zeit-Dilationen erzeugt, bilden sie im Zentrum der Tetraeder-Zwischenräume, also den Oktaedern, eine Anomalität, die in der 3-Farbenstruktur des Oktaeders die 4. Farbe als Manko-Farbe im Zentrum erzeugt. Diese ist eine komprimierte Eigenschaft bzw. Moment, die sich nur als Punktgröße auswirken kann. Diese Punktgröße aber ist der Vektor in die 4. Raumdimension, da ein Punkt ja kein Vektor sein kann. Als solche ist sie eine lokale Oszillation der Matrix-Struktur. Wird die Matrix-Struktur jedoch nicht erkannt und als eine Leere des Raumes gesehen, dann wird diese lokale Oszillation zu einem separaten Teilchen. Zudem kann die hohe Frequenz der Oszillation ebenfalls nicht erkannt werden, wodurch dann die Paritäten zu speziellen Eigenschaften des Teilchens werden.
Die Paritäten werden durch den 4 Farben-Zyklus erzeugt und bilden eine Doppel-Oszillation zwischen Energie-Dicht und (+/-) Zeit. Der Maßstab in der Matrix erzeugt die Energie-Größe der Teilchen und daher die Teilchenart. Weitere sekundäre Resonanzen im 3D-Raum erzeigen weitere Eigenschaften, die im Teil 4 beschrieben werden.
Diese Teilchen, die Fermionen, werden von der heutigen Physik als separate Teilchen gesehen, obwohl sie nur Stör-Momente in der vibrierenden Matrix-Struktur sind. Seit Tausende von Jahren der menschlichen Geschichte wurde nur der leere Raum gefüllt von ihm separierten Teilchen gesehen, ohne zu erkennen, dass die Teilchen nur die Störung des Raumes (oder des „Nichts“ nach ihrer Auffassung) sind. Die Physik ist hier an eine Grenze der Erkenntnis gekommen. Ohne die Anerkennung einer Raum-Zeit-Pulse Struktur der Matrix, können keine wirklichen Fortschritte in der Physik erwartet werden.
Das Ende der Geschichte ergibt erschreckende Resultate. Es gibt keine Teilchen, keine Leere des Raumes, ja keine Zwischenräume überhaupt. Unser physikalisches Universum existiert als ein separates Ding nicht wirklich. Wir sind nur Eigenschaften eines Mediums, einer niemals direkt erfahrbaren Wirklichkeit. Wir sind nur das Lied, nicht der Sänger. Diese schreckliche Erkenntnis, die unseren Hochmut bricht, hat aber auch Vorteile. Kennen wir das Medium, erkennen wir die Matrix, so meistern wir die Trägheit, Raum und Zeit. Wir geben unserer Wissenschaft und Physik die Chance, Antigravitation und Zeit-Verschiebungen zu erforschen, Dinge, die ein heutiger Physiker noch nicht einmal aussprechen würde.
Teil 3 versuchte, uns mehr Handwerkszeug für die Sicht auf Fermions zu geben, die im Teil 4 behandelt werden sollen. Es wurde versucht, eine durchgehende kausale Linie von der Quantentheorie bis zum Maßstab unserer natürlichen Umgebung aufzuzeigen. Sie basiert auf eine Struktur im Kleinsten, die aus Raum, Zeit und Puls begründet wird. Diese 3 Begriffe können nur mit sich selbst erklärt werden. Sie sind an der Basis alle invariant. Dadurch kann der Raum mit Zeit, die Zeit mit Raum erklärt werden. Der Puls aber kommt aus dem 4D-Raum, seine Größe kann daher nicht direkt von Raum und Zeit abgeleitet werden. Irgendwann in der Zukunft wird auch der 4D-Raum von uns kontrollierbar, dann bleibt für eine Erklärung nur der Wiederstand des Mediums unseres Universums, seine Puls erzeugende Elastizität als ein Axiom.
