Teilchen sind Begleitphänomene der Feldtheorie. Das Schrödinger-Feld ist daher ein raumfüllendes physikalisches Feld, dessen Wert an jedem Punkt im Raum die Wahrscheinlichkeitsamplitude einer Wechselwirkung an diesem Punkt ist.. Elizabeth A. Hobson
Ein Feld im Kontext der Matrix ist eine Vektor- und Tensor-Oszillation in einem 4-dimensionalen Raum, dessen Dichte und Energie von λ (Wellenlänge) seiner Oszillation abhängt. Mit der Quantelung von λ werden Raum, Zeit und seine Energie ebenfalls zu Qanten. Deshalb wird in der Matrix nicht jeder (oder irgend ein) Punkt, sondern nur Matrix-Punkte gesehen.
Im Teil 4 sollen nun die „Teilchen“ Quarks, Protonen, Neutronen, Elektronen, Neutrinos mit all ihren Antiteilchen raum-, zeit- und kraftgeometrisch beschrieben werden. Sie sollen aus einen stabilen Zustand der Matrix erklärt werden. Die Vorbedingungen, die Paradigmen wurden in den Teilen 1-3 beschrieben. Hier kurz angesprochen:
Die Dimension Null mit Wert 0 bekommt in der Multiplikation einen Wert
(die Existenz).
Die daraus entstehenden 3 Raumdimensionen bilden unseren bewussten Raum.
Massen und Trägheit sind die Einwirkung der 4. Raumdimension.
Zeit ist immer die Einwirkung der nächst höheren Dimension.
Ursache ist c, die Limitierung der Gleichzeitigkeit.
Unser universeller Zyklus (5. Dimension) ist momentan die (+) Zeit.
Eine 4D Oszillation V<c würde eine (-) und eine (+) Zeit erlauben.
Die Super-Symmetrie (SUSY) ist die Sicht aus der (-) Zeit.
Die (-) Zeit macht den vollen Zyklus (Spin 1) zum Equilibrium
“Ein Partikel ist hier nicht ein seperates Feld, es ist der Zustand des Mediums an diesem Ort.
Aus diesem Blickwinkel entstehen in CERN keine neuen Partikel, es ändert sich nur der Zustand des Ortes. Alle Kräfte, alle Wechselwirkungen gehen aus den Störungen der ursprünglichen Oszillation des Raumes, der Zeit (auch sie oszilliert) und des Pulses hervor.
Eine Stehende Welle ist die Oszillation mit Vektor (als Tensor) in die 4.Dimension.
Was sagt die moderne Teilchenphysik:
Traruh Synred, Ph.D. in Particle Physics meint: Wie alle
Wellenfunktionen von Teilchen bedeuten sie nur die Wahrscheinlichkeit, eines
dort zu finden. Teilchen existieren überall dort, wo ihre Wellenfunktion
Null ist. Ein Teilchen ist die Vibration/Welle, die an mehreren Orten
gleichzeitig sein kann. Die Schwierigkeit ist, das Teilchen nur an einen Ort
zu finden. Die Wahrscheinlichkeit des Ortes wird mit der Born Regel gegeben
... (der Wert des absoluten Wertes der Wellenfunktion quadriert). Aus
historischer Sicht bezeichnete "Teilchen" sind eben keine Kügelchen.
Was als leerer Raum betrachtet wird, ist nur die Manifestation noch nicht erwachter Materie. Nikola Tesla
Ein tiefer Blick auf das Medium aus dem die Partikel bestehen
Die Tetraeder-Oktaeder Struktur der Matrix erlaubt 2 verschiedene Raumstrukturen, die je nach Blick-Winkel sichtbar werden. Der Tetraeder-Raum hat eine 60° Struktur und der Oktaeder-Raum eine 90° Struktur. Es ist die gleiche Raumstruktur. Je nachdem die Tetraeder oder Oktaeder markiert werden, wird die Struktur zu Tetraeder mit Zwischenräumen in Form von Oktaeder oder zu Oktaeder mit Zwischenräumen in Form von Tetraeder. Beide Sichtweisen werden MATRIX genannt.
Mit diesen Paradigmen sollen alle Kräfte, Ladungen und Teilchen sowie die Photons beschrieben werden. Diese Beschreibung zeigt eine grundsätzliche Lösung ohne eine Quantifizierung. Die Messweisen in Coulomb oder Newton werden nicht angewandt, das Planck’sche Wirkungs-Quant h wird als Einheit verwendet. h = E·ʎ/c, ein immer gleicher Moment in Lichtgeschwindigkeit.
Die MFT (Matrix Feld Theorie) als Theorie neuer Paradigmen zeigt im Folgenden den physikalischen Hintergrund.
 Die Kanten der Strukturen
sind Verbindungslinien zwischen den Feldern, hier als 4 farbige Sphären
dargestellt. Die 4 Farben sind die Zustände (++) (+-) (-+) (- -), die in der
Matrix ein Equilibrium in Raum-Zeit und Pulse ergeben. Die Eigenart des
Equilibriums erlaubt theoretisch jede Dichte, Stärke und Größe einer
Energie, ohne eine Wirkung auf benachbarte Räume zu haben. Es kann jede
Skalierung ertragen, wobei die Abstände theoretisch jede Größe haben können,
auch die Planck´sche Länge (1,616·10^−32 mm). Damit werden Energien von
e=h·c/ʎ =~1.5·10^15 MeV festgehalten. Die Bedeutung dieser Zahlen ist schwer
abschätzbar, da alles unvorstellbar klein und nur theoretisch erfassbar ist.
Dabei muss im Auge behalten werden, dass alles oszilliert und die Farben im
Maßstab der Planck’schen Länge Lᵨ innerhalb von Lᵨ/c oder ~3·10^-33 sec
wechseln. Aus diesem Grund arbeiten wir hier mit dem Maßstab S1 der Matrix,
den Maßstab des Protons und den invariable Planck’sche Wirkungsgrad h.
Die Kanten der Strukturen
sind Verbindungslinien zwischen den Feldern, hier als 4 farbige Sphären
dargestellt. Die 4 Farben sind die Zustände (++) (+-) (-+) (- -), die in der
Matrix ein Equilibrium in Raum-Zeit und Pulse ergeben. Die Eigenart des
Equilibriums erlaubt theoretisch jede Dichte, Stärke und Größe einer
Energie, ohne eine Wirkung auf benachbarte Räume zu haben. Es kann jede
Skalierung ertragen, wobei die Abstände theoretisch jede Größe haben können,
auch die Planck´sche Länge (1,616·10^−32 mm). Damit werden Energien von
e=h·c/ʎ =~1.5·10^15 MeV festgehalten. Die Bedeutung dieser Zahlen ist schwer
abschätzbar, da alles unvorstellbar klein und nur theoretisch erfassbar ist.
Dabei muss im Auge behalten werden, dass alles oszilliert und die Farben im
Maßstab der Planck’schen Länge Lᵨ innerhalb von Lᵨ/c oder ~3·10^-33 sec
wechseln. Aus diesem Grund arbeiten wir hier mit dem Maßstab S1 der Matrix,
den Maßstab des Protons und den invariable Planck’sche Wirkungsgrad h.
Das Basis-Medium liegt im Feld-Maßstab 1
Wenn Puls und Abstand variabel sind und h invariabel dann wird Pulse zu unendlich beim Abstand 0. Es ist klar, dass das keinen Sinn macht. Eine kleinste Größe ist gefordert, die bei weiteren Betrachtungen als Referenz gelten kann. Das Standard Modell (SM) setzt hier die Planck Einheiten Länge = 1.6·10-25 m, Masse = 2.2·10-8 kg und Zeit = 5.4·10-44 s ein. Da diese Werte immer noch die die Referenz unserer normalen Welt (m, kg, s) verwenden, machen sie für uns keinen Sinn, da sie ja in der betrachteten Größenordnung der Matrix zu stark von der Relativitätstheorie bzw. dem Lorentz-Faktor verzerrt werden. Der im Bereich (m, kg, s) isotropisch erscheinende Raum wird hier gequantelt und ist nicht mehr länger isotropisch.
Hier sollen zuerst die geometrischen Bezüge als Basis des Verstehens gezeigt werden, um danach als separaten Abschnitt die relativistische Verzerrung mit einzubeziehen. Es machte für mich daher Sinn, die Feldgröße eines Protons als Matrix-Maßstab S1 anzunehmen um die geometrischen Bezüge anderer Felder wie S2, S3, S4 usw. zu erklären.

Das obere Bild demonstriert deutlich die Sichtweise des triangulären und des orthogonalen Raumes. Es ist die gleiche Raumstruktur. Einmal werden die Stadien des Raumes als bunte Kugeln in Beziehung gebracht, ein anderes Mal werden die gleichfarbigen Diagonalen gezeigt, die ich hier als Autobahn gleicher Energien bezeichne. Es zeigt auch einen separat dargestellten Oktaeder, der aneinander gereiht wiederum eine orthogonale Struktur bilden würde, die jedoch einen anderen Winkel hat. All das sind Sichtweisen derselben Raumstruktur.
Geometrische Zusammenhänge der Dimensions-Darstellungen
Die Erkenntnis einer Dimension ist das Verstehen seiner Geometrie. Als erstes Axiom muss der Dimension D0 eine Größe zuerkannt werden. Erst dann ist sie existent (siehe MATRIX1 Dimensionen) Erst dann können die Bedingungen der Dimension D1 erfüllt werden. Erst dann können sich x-beliebig Dimensionen als Erkenntnis-Grade manifestieren. Die Matrix-Theorie gibt uns die Regeln einer exakten Betrachtung von 4 Dimensionen.
1.) Gleiche Stablängen in einem Maßstab, bzw. dessen Einbruch in kürzeren Längen mit dem Verhältnis 1/3. Damit werden die Bedingungen des Equilibriums der Matrix nicht verletzt.
2.) Alles oszilliert. Auch hier gilt als Maß die Frequenz. Es oszilliert daher der Raum, die Zeit und die Energie. Die Summe der Zustände in einer Oszillationen ist immer null.
3.) Alle Betrachtungen gelten nur für stabile Zustände. Die Stablängen (λ) und ihre Frequenzen haben das Verhältnis 1/3^x (1-3-9-27-81 usw.).
4.) Diese Bedingungen gehen durch alle Dimensionen. Der Kollaps in eine andere Dimension findet sich in eine neue mehrdimensionale Harmonie bzw. Stabilität wieder.
 Beispiel 1: Die Stablänge 3 wird zur Stablänge 1 zusammen gedrückt. Als
Graphik auf der Fläche D2 besteht die Möglichkeit, die Verkürzung von S9 zu
S3 so darzustellen, dass das Aufbiegen in die neue Dimension D2 wieder
stabile Stablängen (S1) haben kann. Dabei muss bewusst werden, dass von D1
aus dieses Aufbiegen als imaginärer Wert (Tenso) erscheint. Der imaginäre Wert wäre
hier die Aufbiege-Höhe H1=√(1^2– 0.5^2) = 0.866
Beispiel 1: Die Stablänge 3 wird zur Stablänge 1 zusammen gedrückt. Als
Graphik auf der Fläche D2 besteht die Möglichkeit, die Verkürzung von S9 zu
S3 so darzustellen, dass das Aufbiegen in die neue Dimension D2 wieder
stabile Stablängen (S1) haben kann. Dabei muss bewusst werden, dass von D1
aus dieses Aufbiegen als imaginärer Wert (Tenso) erscheint. Der imaginäre Wert wäre
hier die Aufbiege-Höhe H1=√(1^2– 0.5^2) = 0.866
 Beispiel 2: Hier wird nur der zusammengedrückte Teil gezeigt (weiße Struktur in D2).
Die Darstellung in D3 erlaubt aber hier das Aufbiegen zur nächst höheren
Dimension zu zeigen. Gleichzeitig kann die Aufbiege-Höhe mit der Farbe Gelb
oder Grün als Vektor des imaginären Aufbiegens gegen Kompression oder
Dekompression gezeigt werden, wenn die Vertikale der Indikator von Druck/Depression ist. Die weiße Struktur wäre dann der statisch wirkende
Null-Wert des Raumes. Es entsteht die Aufbiege-Höhen H2=√(H1^2 –
(0.5·H1)^2) = 0.7806. H1 wäre der imaginäre Wert in D1
richtung D2 und H2 der
imaginäre Wert in D2 in Richtung D3.
Beispiel 2: Hier wird nur der zusammengedrückte Teil gezeigt (weiße Struktur in D2).
Die Darstellung in D3 erlaubt aber hier das Aufbiegen zur nächst höheren
Dimension zu zeigen. Gleichzeitig kann die Aufbiege-Höhe mit der Farbe Gelb
oder Grün als Vektor des imaginären Aufbiegens gegen Kompression oder
Dekompression gezeigt werden, wenn die Vertikale der Indikator von Druck/Depression ist. Die weiße Struktur wäre dann der statisch wirkende
Null-Wert des Raumes. Es entsteht die Aufbiege-Höhen H2=√(H1^2 –
(0.5·H1)^2) = 0.7806. H1 wäre der imaginäre Wert in D1
richtung D2 und H2 der
imaginäre Wert in D2 in Richtung D3.

Beispiel 3: Die Oktaeder mit den Stablängen in Weiß zeigen den zusammengedrückten Bereich in D3. Der Oktaeder besteht aus nur 3 Farben. Er ist der Zwischenraum von 8 Tetraedern, die jedoch aus 4 Farben bestehen. Man muss sich den Raum D3 als Netzwerk von Tetraedern vorstellen, wo die Oktaeder nur Zwischenraum sind. Trotzdem spielt sich der Prozess des Energieausgleiches in den Oktaedern ab. In ihren Zentren bildet sich die fehlende 4. Farbe der 3 Oktaeder-Farben als Energieausgleich. Dieser ist hier als Kugeln in Grün und Gelb dargestellt. In ihnen spielt sich der Kollaps in D4 als Ausgleich ab. Da eine Isometrie auf einer D2 Fläche keine Möglichkeit hat, den Vektor in D4 darzustellen, bleiben die D4 Vektoren (Tensoren) imaginär.
Im oberen Bild wird versucht, die senkrecht zu den Diagonalen
stehenden Vektoren nach D4 als Fläche auf den Diagonalen darzustellen.
Die
Höhe des Aufbiegens wäre hier H3=√(H2^2 –
(0.5·H2)^2) = 0.6760. H3 wäre der
imaginäre Wert in D2 nach D3. H3 wäre der imaginäre Wert in D3 in Richtung D4.
In jeder Dimension sind imaginäre Tensoren der nächst höheren Dimension möglich.
Kollaps der Stabkraft und das Aufbiegen in die 4. Raumdimension
In jedem Maßstab herrscht ein Equilibrium der 4 Zustände, die Paritäten einer Oszillation sind. Trotzdem werden Störungen aus der Umgebung in die Equilibrium-Systeme der Tetraeder und Oktaeder eingebracht. Das System (z.B. Oktaeder) verändert seinen Zustand entsprechend. Es transmittiert diese Störungen zurück in die Umgebung. Während dieser Prozessdauer entsteht im Zentrum der Oktaeder ein resultierendes Moment, die Manko-Farbe. Wie in Maßstab vorher gezeigt, sind die geradzahligen Maßstäbe S2; S4; S6 usw. nicht fähig, Störungen aufzunehmen. Sie transmittieren sie mit V=c in den umgebenden Raum der Matrix. Im Zentrum der betroffenen Oktaeder aber können die kulminierenden Kräfte der Stauchung (der Diagonalen) zu einer punktförmigen Einbiegung in die 4. Raumdimension führen. Nun, wann genau passiert das?
Die Versuche in CERN zeigen, dass kinetische Energie sich in Masse umwandelt. Es entstehen neue Teilchen. Den gleichen Prozess nimmt man im Zentrum von Galaxien an. Die BB-Theorie nimmt einen umgekehrten Prozess an; aus einer Hyper-Dichte werden Energie als Masse entlassen, die Geburt der Fermionen.
 Die
Matrix Theorie nimmt an, dass der Input der 4D-Strahlung mit V=c
rechtwinklig zur 3D-Raum-Oszillationen das Phänomen der Partikel erzeugt.
Genaugenommen ist es eine Doppel-Oszillation, die Tensor-Oszillation
(D4) und die 3D-Vektor-Oszillation der Partikel-Felder
(Raum-Kompression/Depression). Es sind die 4 Zustände, die an
den Ecken eines Tetraeders als summmarischen Werl ein Equilibrium bilden.
Die
Matrix Theorie nimmt an, dass der Input der 4D-Strahlung mit V=c
rechtwinklig zur 3D-Raum-Oszillationen das Phänomen der Partikel erzeugt.
Genaugenommen ist es eine Doppel-Oszillation, die Tensor-Oszillation
(D4) und die 3D-Vektor-Oszillation der Partikel-Felder
(Raum-Kompression/Depression). Es sind die 4 Zustände, die an
den Ecken eines Tetraeders als summmarischen Werl ein Equilibrium bilden.
Da die Fluktuation als Tensorwerte in die 3D-Lokalität zumindest nicht direkt einen energetischen Einfluss auf den 3D-Raum haben kann (rechtwinkliger Vektor), wirkt es dort als Zeit-Puls, dessen Wirkung nur im Wechsel von lokalen Gleichzeitigkeiten erklärbar wird. Aber ja, da hat sich selbst Stephen Hawking den Zahn ausgebissen.
Wie kann sich der Kollaps diagonaler Stabkräfte in die 4. Dimension vorgestellt werden?
Das Phänomen Stabkraft entsteht aus 2 Eigenschaften:
1. Wiederstand oder Elastizität des Stab-Mediums (W=δ*L)
2. Die
Knick-Kraft (KK), ein Moment p=hc/ʎ=1 Quant
Während W der Widerstand des Mediums ist, ist die Energie eines einzelnen
Stabes kontra-proportional zur Stablänge d (p=hc/ʎ). Damit kann in einem
Diagramm der Maßstab als Vertikale und der Wiederstand als Horizontale
gesehen werden. W würde dort eine horizontale Parallele zu S(x) gesehen,
während KK wegen der Geometrie der Matrix dort wäre eine progressive Kurve. Die
2 Kurven werden sich zwangsläufig da schneiden, wo ein Aufbiegen der
Stabkraft in die D4 zu erwarten ist (siehe untere Liste).
Die Liste zeigt die die alten
Werte des Standard-Modells (SM) mit den nun neuen Werten. Die neuen Werte
sind die Umsetzung der Werte der SPIN-Theorie zu Paritäten der Oszillationen.
Die Werte der alten Idee der Super-Symmetrie (SUSI) werden zu Paritäten der
(+) und (-) Zeit. Der Kollaps als ein Aufbiegen in die 4. Raumdimension
ergibt das Phänomen Masse und Trägheit.

A prima Vista werden die Quarks vermisst. Spin und Ladung fallen weg. Alle Partikel-Eigenschaften wurden zu Zustände ein und desselben Raumes. Die Lila hinterlegten Werte sind die der Manko-Farbe und somit Tensor-Werte aus der 4. Dimension. Sie sind Werte, die als Masse und Trägheit interpretiert werden. Alle Partikel-Formen sind nun Oszillationen der Matrix.
Die neue Liste
1.) Es zeigt die neuen Werte im Zusammenhang mit der Geometrie der
Matrix.
2.) Die neuen Werte nehmen die Begriffe Spin und Ladung nicht
auf.
3.) Es zeigt die alten Werte Materie und Antimaterie (Schwarz und
Blau)
4.) Es zeigt in den neuen Werten (+) Zeit und (-) Zeit anstatt
Materie und Antimaterie
5.) Es werden keine Quarks aufgeführt. Dies wird
später separat erklärt.
6.) Es wird kein Neutron aufgeführt. Dies wird im
Absatz Beta Zerfall erklärt.
Die Erklärung der Liste:
Von links nach rechts:
• Die Massstäbe S1 bis S18 (senkrecht)
• Es zeigt ein vertikal aufgeführtes
Diagramm. Dort gilt Orange der Stab-Wiederstand der Matrix als
allgemeine Eigenschaft des Raumes. Ab S6 werden Balken gezeigt. Sie
symbolisieren den Kollaps in 4D als Tensor. Da dieser abhängig von der Stablänge ist
(p=h/ʎ), ergibt es hier eine exponentielle Kurve, die sich mit der
Niveau-Kurve des Widerstandes schneidet.
• Die Markierung Hadronen zu
Bosonen (Quants).
• Die Liste der Hadronen und Bosonen.
• Die alten
Quantenwerte Ladung und Spin
• Die neuen Werte der Doppel-Oszillation + -
in der (+) Zeit + - in der (-) Zeit.
• Die Zuordnung zur Matrix-Geometrie
Die Matrix-Theorie erklärt das neue Konzept der Ladung: Ladung
In dem Sinne wird ebenfalls der Spin neu interpretiert: Spin
Die Geometrie der Matrix, ihre Doppel-Oszillation erfordert den Einbezug der Antimaterie als eine integre Eigenschaft jeder Materie oder jeden Teilchens. SUSI
Die Frontwelle der radialen Expansion des Urknalls aus der 4. Raumdimension (siehe Die wahre Natur des Universums) erschafft die Gleichzeitigkeit und die Erkenntnis-Fähigkeit unseres 3D Universums. Die Rückseite dieser Frontwelle, eine Sicht von Innen aus der expandierenden 4D-Sphäre, ist der Hyperraum. Aus dieser Sicht ist jedes Materie-Teilchen auch Antimaterie.
Antimaterie ist die Rückseite der Materie und von ihr nicht trennbar.
Das Feuerwerk der “Large Hadron Collider “ neu interpretiert

Erinnern wir uns auf die Bedingung Einsteins für den Raum an sich. Der Matrix Raum
“Nichts ist wichtiger als die Tatsache, dass der Raum nicht leer ist. Er ist die Substanz der mächtigsten physikalischen Kräfte.” - John Archibald Wheeler
Die Matrix-Theorie akzeptiert keine separaten Felder oder Räume, d.h. keine vollkommen losgelösten Raumteile mit unabhängigen Eigenschaften, die im SM (Standard Modell) als Quanten-Zahlen festgelegt sind. Sämtliche als Quantenzahlen festgelegten Eigenschaften sind eigentlich lokale Eigenschaften des Raumes, der so als Medium der oszillierenden Momente dient. Ein Teilchen in der Matrix ist daher nur der Ort, an dem die Momente, seine Schwingungs-Werte, seine Zustandsbeziehung zur umliegenden Raum-Entropie, sein Farbwert der QCD usw. als das spezifische Teilchen erkannt wird.
Ein Teilchen ist die Schwingungsenergie, das Momentum der Störung des Raumes bzw. der Ausgleichsmoment der 3 Momente des Oktaeders, der als Raumzelle das Teilchen einschliest. Damit gibt es ausser Energie nichts anderes, was unsere physikalische Welt ausmacht.
Ein Teilchen bahnt sich daher nicht einen Weg durch den Raum, indem es ihn auseinander schiebt, es propagiert als ein Bündel von Momenten durch die Struktur, die das Medium des Raumes bildet. Die Matrix besteht aus einer Struktur in verschiedenen Maßstäben, die bezüglich der Grund-Frequenz eine verschiedene Resonanz bildet und daher auch eine eigene Metrik. Nach wie vor gilt dort ebenfalls die Planck-Konstante h. Dadurch entstehen maßstabsabhängige Energie-Dichten, d.h. Stablängen der Netzknoten, Frequenzen die von der Resonanz zur Basis-Frequenz verstärkt oder unterdrückt werden, siehe Der Matrix Maßstab . Auch die relativistischen Wertveränderungen (Lorentz-Faktor) werden durch die Maßstäbe quantisiert. Hier heißt das, dass die Werte innerhalb eines Maßstabes und daher innerhalb einer Frequenz gleich bleiben und dort feste Werte haben. Die Ratio zweier solcher Werte (zweier Maßstäbe) müsste jedoch eine Integer-Zahl sein.
Das große Bild zeigt, dass mit der Matrix
Raum-Struktur und seine integren Werte eine lokale Zerstörung ebenfalls nur
strukturelle Trümmer mit integren Werten erzeugen kann. Wie vorher erwähnt,
werden Quarks wohl von den 3 Diagonalen der Oktaeder ableitbar, Gluonen aber
von den Stablängen der Tetraeder. Die Maßstäbe haben jedoch verschiedene
Energiewerte, wodurch Gluonen als Träger verschiedener Energien gesehen
werden. Die Sache wird jedoch noch komplizierter, wenn e=h▪f konsequent
angewendet wird. Dann ist es die (meist kinetische) Energie des Geschosses,
die die Stablänge des Trümmerteils bestimmt (λ=c/f => λ=c▪h/e). So entstehen
die Teilchen-Generationen des SM. Es ist klar, dass die chromo-dynamischen
Werte der QCD von den Farben der Matrix her kommen (++
+- -+
- -).
Im SM werden sie als ↑↑ ↑↓ ↓↑ ↓↓ dargestellt.
Rechnerisch sind zwar die Quarks als 1 bewertet, in der Matrix jedoch als
1/√2. Das kommt daher, dass in der Matrix alle Werte auf den Maßstab S1 mit
Stablänge 1 abgestellt werden. Die Diagonalen wirken mit der ½ Distanz (1/√2
oder 1/2•√2) zum Zentrum der Manko-Farbe. Die Abstände der Knoten des
Oktaeders in S1 haben jedoch die Größe 1. Das SM jedoch setzt die Referenz
auf die Quarks, die dort in ihrer Theoretisierung der QCD den Wert 1
bekommen. Dadurch werden alle Werte der anderen Stablängen in der QCD zu
1/√2. Es ist theoretisch nicht falsch aber unpraktisch. Es wird im SM davon
ausgegangen, dass Quarks die Basis unserer materiellen Welt bilden. Das
jedoch ist eine Sackgasse des Denkens. Wie kann ein Basis-Element eine
Lebensdauer von 10^-25 sec. haben und dabei ca. 200 Mal größer
(Compton wavelength) als sein
Behälter, dem Proton sein. Wobei die Lebenszeit eines Protons ca. > 10^50
Mal länger dauert als die der Quarks !?.
Das Ende der Geschichte ist, dass die Matrix durch keine noch so große Geschoss-Energie geändert werden kann, dass der Oktaeder des Protons von seinen spezifischen Momenten zwar frei geschossen, jedoch nicht vernichtet werden kann. Das Energiegeschoss besteht ebenfalls aus ein Bündel von Momenten, die mit aller Härte auf die Momente des Ziels stoßen und dort sternförmig in ein buntes Feuerwerk explodieren, wobei alle Mitspieler dieses Spiels Momente sind und nur von ihrer Stellung und Bezug zur Matrix sogenannte intrinsische Werte bekommen. So werden sie von uns falsch als individuelle Teilchen und ihre wahre Natur, die Matrix aber nur als Leere gesehen.
Es ist der „leere“ Raum Einsteins, der den Äther ersetzt und unsere scheinbare Wahrheit zu einem relativen Scheinbild werden lässt. Der Raum ist das Medium und es gibt kein Loch im Raum.
Die Fermionen
Die Fermionen sind, wie im Vorgehenden beschrieben, die Wirkungs-Feld-Zentren eines 4D-Moments in der 3D-Raum-Ebene. Sie sind also nicht wirklich im 3D-Raum existent, haben jedoch dort Wirkung. Sie lassen sich prinzipiell nicht direkt durch Energien des 3D-Raumes bewegen, sondern nur durch die Verformung der 3D-Raum-Ebene, die jedoch der Limit V=c unterliegt. Unter dem Aspekt, dass Bosonen die 3D-Wechselwirkung zwischen den Fermionen sind, sind sie an die wechselwirkenden Felder der Fermionen gebunden und daher in ihrer Reichweite limitiert. Fermionen sind daher Verformungen des 3D-Raumes. Es sind die Ladungsfelder um diese Kraftzentren, die primären und sekundären Feld-Hierarchien, die für komplexere Strukturen verantwortlich sind.
Das Standard Modell kennt durch die geschichtliche Tradition der zeitlich getrennten Entdeckungen eine Anzahl von Kriterien, die nur schwer zu korrelieren sind. Hier aufgezählt:
Spin --------------------------------- Drehung 720° auf 360° reduziert, daher 1/2 Spin
Chiralität, Helizität ----------------Drehung links-rechts im 3D-Raum (Handregel)
Antimaterie -------------------------alle Quantenwerte (inkl. Zeit) werden umgekehrt
Ladung ------------------------------innere Eigenschaft der Fermions
Daraus hat Dirac seine Spinoren ableiten können. All
diese Werte mit naiven Namen bekamen nun einen mathematischen Zusammenhang.
Auch die Matrix Theorie leitete die 4 Momente im 4D-Raum als Vorzeichen
der Raumdichte ab, (++) (+-) (-+)
(- -) bzw. als Paritäten hier Farben
(++) (+-)
(-+) (-
-)
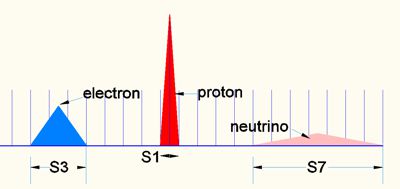 Bild 8
Bild 8
Hier werden die 3 Partikel vom SM (Standard Model) abgeleitet. Vertikal der 4D-Moment (E) und horizontal die relative Feldgröße in 3D. Die Werte sind hier symbolisch.
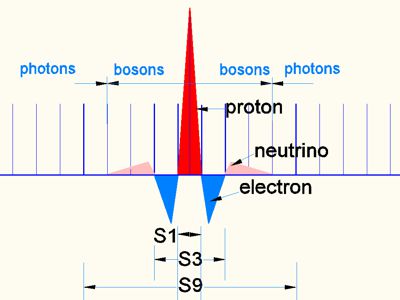 Bild 9
Bild 9
Es zeigt das Proton (rot) mit dem Elektron-Para Feld (blau) und dem
Neutrino-Para Feld (hellrot) in der Matrix. Parafelder sind die logische Konsequenz der
Matrix. Sie entsprechen hier der Formel λC
= h/(c · m0) der Compton Wellenlänge.
Während im SM der Impakt des
Partikels abrupt von dem Nachbar-Raum abgeschnitten wurde, dehnen sich seine
Nebeneffekte im Matrix-Raum bis zum Neutrinofeld aus. Nach dem Neutrinofeld
werden die Nebeneffekte des Impakts als Photonen weiter getragen. Daher hat
z.B. ein Proton ein Positron und ein Anti-Neutrino (siehe auch β+ Zerfall).
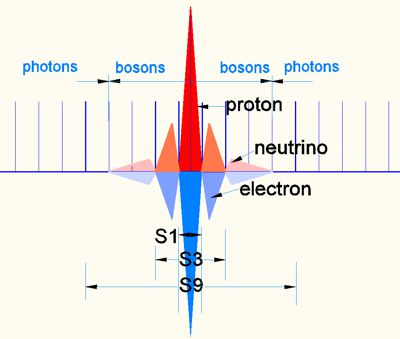 Bild 10
Bild 10
Während Bild 9 symbolisch nur 1/2 Zyklus zeigt, wird hier der ganze Zyklus (+ und - Zeit)aufgezeigt. Es sind die Para Felder der Doppel-Oszillation. Alle Felder und Para Felder heben sich energetisch auf. Ab S9 können keine Bosonen mehr gebildet werden und EM-Schwingungen der Photonen entweichen in den EM-Raum.
Die Familienbeziehungen der Fermionen
In diesem Beitrag wird eine symbolische Graphik angewendet, um die signifikanten Unterschiede zwischen den Fermionen zu erklären. Die Raute symbolisiert ein Oktaeder. Seine 3 Diagonalen (hier nur 2 dargestellt) werden durch die Pfeile symbolisiert. Die blauen und grünen Punkte zeigen die Parität der Raumzellen im S1 (Maßstab 1). Hier wird deutlich, dass in Richtung der Pfeile immer nur eine Farbe angegeben wurde. Es sind die Diagonalen, die asymmetrische Energien in die Umgebung mit V=c auslaufen lassen. Sie sind die als Quarks bezeichneten Trümmer der LHC-Forschung. Der zentrale Punkt zeigt das Moment in D4, dass das Phänomen der Masse erzeugt. Die Linien zeigen das Oktaeder, dass das Primärfeld bildet. Seine Farbe zeigt seine momentane Parität in Bezug zum Proton.

Die Protonen sind die Ur-Rasse. Sie haben die Stablänge der Raumgröße S1 . S1 ist die erste Größe des Tetraeder-Raumes, die auch als Unit 1 (U1) bezeichnet werden kann, da sie mit den 4 Farben die 1. Einheits-Größe bilden. Nach den Forschungen der Teilchenphysik gibt es weitere Familien-Beziehungen, die jedoch unstabil sind und keine komplexen Strukturen bilden. Die philosophische Basis der Matrix Theorie verlangt eine harmonische Beziehung bzw. Resonanz zur direkten Umgebung. Die Bedingung, dass alles, das Medium sowie seine Störungen in einer ausgleichenden Beziehung steht, dessen Resultat Null ergibt, lassen umgebende Sekundär-Felder als Oszillationen erwarten. Diese können nur in S3, S5: S7 erwartet werden, da in diesem Maßstäben die geometrischen Formen (hier Oktaeder) das gleiche Zentrum haben und ihre Ausgleichs-Energien als Boson nicht in die Umgebung entweichen können. Hier wird deutlich, dass im Grunde alle Fermionen eine gleiche geometrische Form haben. Sie unterscheiden sich nur, in welcher Tiefe der Moment zur 4. Dimension liegt. Die sich dadurch ergebende Unterschiede liegen daher in den Sekundär-Feldern (Parafelder), dessen Parität der eigentlichen Unterschied ist. Z.B. wenn S1=(+) ist, dann ist S3=(-) und S5=(+) usw.

Das Neutron besteht aus 1 Proton und einem Elektron. Der Grund für diese Verschmelzung liegt im Sekundärfeld des Protons. Es steht im Zusammenhang mit Zuständen höchsten Drucks während der Geburt des Universums oder mit Zuständen innerhalb von Neutronensternen während des Kollapses zu einer Supernova. Die Teilchen dort stehen unter einem solchen Druck, dass Elektronen gezwungen sind, das Feld S3 um das Proton (S1) herum zu konvergieren. Nach dem Kollaps in S3 hat das Elektron dasselbe Zentrum wie das Proton, jedoch auf der (-) Zeitparität seiner Schwingung. Ein Neutron erlangt daher ein Gleichgewicht in S3 und den nachfolgenden Parafeldern S9-S27. Im Standardmodell ist es der β+ Zerfall. Die entsprechenden Feynman-Diagramme legen nahe, dass auch die nachfolgenden S5-S7 betroffen sind. Leider gehen alle Feynman-Diagramme davon aus, dass es keine Protonen gibt, und zeigen stattdessen nur die 3 LHC-Trümmer als Quarks, wobei nur ein Quark mutiert. Es ist die alte klassische Vorstellung, dass selbst das kleinste Teilchen in noch kleinere Teilchen zersplittert werden kann. Teilchen jedoch sind nur Energie der Felder. Daher gilt hier: je höher die Energie, je kleiner das Teilchen, Deshalb ist es Unsinn, dass die wesentlich grösseren Quarks in einem Proton sein könnten.

Das Elektron ist der kleine Bruder des Protons, es ist vollkommen gleich, jedoch verpackt in einem Oktaeder der Größe S3. Er hat also die 3-fache Stablänge als Primär-Feld-Umgebung des 4D-Momentes. Dieses Moment ist die Wirkung einer Oszillation mit Vektor vertikal zu den 3D-Kordinaten und hat die Gegenparität der Protonen Oszillation. Verschmolzen mit einem Proton (d.h. es hat das gleiche Zentrum wie das Proton) würde es alle Folgefelder aufheben. Der Normalzustand eines Elektrons ist jedoch eine eigene separate Einheit. Diese wechselwirkt mit den Ladungs-Feldern S9-S27 des Protons und ist verantwortlich für die Wirkungen des Periodischen Systems. Theoretisch hat es als S3 auch Wechselwirkung mit Neutrinos S5 und S7. Wechselwirkungs-Energien sind jedoch dort schon Bosonen und nicht haben keinen Einfluss auf "Ladung".

Das Neutrino ist, wie nebenstehend durch die rote und blaue Linie symbolisiert, in den Oktaeder-Stufen S5 und S7 über dem Elektron etabliert. Es wird in der Tabelle „table of particle“ als Grenzwert zwischen Fermionen und Photonen gesetzt. Es besteht wie das Neutron aus 2 Kraftzentren, die scheinbar allein als Ladungsträger in (+) und (-) Zeit keine Wirkung mehr auf den 3D-Raum haben. Dies wird der wahrscheinliche Grund sein, der uns sie nur die Doppel-Zentren entdecken ließ. Vielleicht wird die experimentelle Physik uns einmal das Ladungs-Neutrino als Bausteine der Aggregats-Zustände nachweisen können. Dass es überhaupt als Teichen und nicht als Boson gilt, hat den Grund, dass in S5 und S7 einen minimalen 4D-Moment hat. Die Zusammenwirkung von S5 und S7 (wie das Neutron S1 mit S3) bewirkt die Neutralisierung der Folge-Felder S9-S27, womit die Ladung entfällt. Dies ist der Grund, weshalb Neutrinos erst spät entdeckt wurden.
Damit sind die symbolischen Bezüge der Partikel zur Matrix-Geometrie aufgezeigt.
Quarks
Für das Verständnis dieses Kapitels sollte unbedingt die Kapitel "Das Feuerwerk der LHC neu interpretiert" -> LHC-Feuerwerk und "Matrix und die Illusion der Partikel" -> Teilchen-Illusion gelesen werden!
Das SM betrachtet die Quarks als die Basis unserer Welt. Und das nur,
weil sie bei der Zertrümmerung der wirklichen Bausteine unserer Welt, der
Protonen gefunden wurden. Dies erzeugte ein nicht zu Ende gedachtes Bild,
was mit gekürten Laureaten fest in das SM genagelt wurde.
Was stimmt noch
nicht: Quarks haben eine Compton Wellenlänge, die ca. 200 mal grösser als
die der Protonen ist. Da in diesen Bereichen des Raumes eine signifikante
Wirkung der GR (Lorentz-Faktor) mit einzurechnen ist, kann auf jeden Fall
gesagt werden, dass Quarks grösser sind als Protonen. Wie passen sie darein?
Quarks müssen unglaublich intelligent sein, damit sie es schaffen, sich in
10^-25 s immer auf eine (+) Ladung zu einigen. Das ist ihre Lebensdauer. Mit
dieser Zeit garantieren sie dem Proton eine fast unendliche Lebenszeit. Sie
sind das Chamelion unter den Partikeln. Sie nehmen je nach Energiegrösse des
zerstörenden Inputs (meist kinetische Energie) Grössen von ca. 2 – 173‘070
MeV an. Sie haben 6 verschiedene Flavour- Zahlen und Ladungsgrössen mit 3
als Divisor. Man kann sie nicht sammeln oder isolieren. Sie sind ein Funke
gewaltiger Zerstörungsprozesse.
Was sind Quarks in der Matrix ?
In der Matrix sind es die Seitenlängen (λC = h/(c · m0)), die Dichte und Energie im Oktaeder des Teilchens (hier im S1 des Protons) bestimmen. In einem Zusammmmenstoss in CERN schlagen unermessliche Energien das Protonenfeld (Oktaeder) tief in die unteren Masssäbe (S3^-x) hinein. Die Elastizität der Matrix fängt diese kinetischen Energien auf und spiegelt sie zurück zu S1, wobei die temporären Energien der Massstabs-Kollapse entlang der 3 Diagonalen des Oktaeders in die Umgebung (Nebelkammer) entweichen. Es ist die Quantennatur der Matrix, welche diese Energien direkt und nicht verwischt (als 3 Paritäten der Raum-Oszilation) entlässt. In der (Mess) Umgebung ausserhalb von S9 (in S1-S9 sind es Bosonen) haben sie den 4D-Moment (Masse) eines Teilchens mit corrilierten S9-S27 Momentum (Ladung). Dies allerdings nur während die kinetische Energie der Matrix-Spigelung noch wirksam ist (~10^-25 s). Die Parität dieser 3 Lichtblitze (Diagonalen des Oktaeders) kann eines dieser Werte (++) (+-) (-+) (- -) haben. Die Chromo-Dynamic der Quarks (Kuark-Törtchen) sollt im Sinn der 3 Kollapse der Massstäbe S1, S-3 und S-9 neu definiert werden. Quarks sind daher Bosonen, Funken brutaler Zerstörung. In CERN werden daher eigentlich keine neuen Teilchen sondern nur neue Laureate erzeugt.

Bosonen
Das Boson ist ein Widerstandsmoment in der Matrix, das bei Verformung den alten Zustand wiederherstellt. Es ist die Matrix, die nur Quanten einer bestimmten Größe E=hc/ʎ zulässt, da seine Stablänge ʎ durch den Massstab definiert ist. Je nach Massstab und Größe der Verformung werden Energien in Quantengrößen freigesetzt, um das Gleichgewicht wiederherzustellen. Es sind die „leeren“ Oktaeder S3-S7 und Tetraeder S2- S6 usw. Die Steilheit der Raumkrümmung, die generell den Feldbereich in den Skalen S1 - S7 begrenzt, verhindern das Ausbrechen dieser kompensierenden Quanten. Ab S9 und als Quanten S8 und größer entweichen sie als Photonen mit V=c . Bosonen sind daher die Photonen in den Massstäben < S9.
 In S1-S7 hat die Matrix wegen der großen
Gravitations-Verzerrung einen Zusammenhang der Kräfte, die auch auf die
Oktaeder und Tetraeder der Umgebung wirken. Die Energie der 4D-Schwingungen
(Zeitvektor) der Oktaeder werden von der Matrix Theorie als
In S1-S7 hat die Matrix wegen der großen
Gravitations-Verzerrung einen Zusammenhang der Kräfte, die auch auf die
Oktaeder und Tetraeder der Umgebung wirken. Die Energie der 4D-Schwingungen
(Zeitvektor) der Oktaeder werden von der Matrix Theorie als
W-Bosonen
interpretiert. Es sind
die normaler Weise „leeren“ Oktaeder, die nun zu Teilchen werden.
Gluonen sind Bosonen, die
bei Wechselwirkungen in Massstäben <S1, also S^-1; S^-3; S^-9 erscheinen.
Natürlich sind diêse Wechselwirkungen ausserhalb natürlicher stabiler
Massstäbe und ein Ergebnis der CERN-Forschung. Dort wurde die Forschung mit
den 4 Paritäten der Oszillation in Zeit und Raum, wie sie die Matrix Theorie
beschreibt, konfrontiert. Das Ergebnis war die Quantenchromodynamik, die
mathematisch die 3 in der Matrix beschriebenen Farben der Oktaeder in ihren
4 Paritäten dargestellt. Das obere Bild zeigt die 3 Farben Rot, Blau, Gelb
mit der Manko-Farbe Grün als Gesamt-Energie des Teilchens (hier der
Oktaeder).
 Hier
eine Darstellung aus
"Quarks - Philoclopedia"
Hier
eine Darstellung aus
"Quarks - Philoclopedia"
Die Quantenchromodynamik zeigt zusätzlich die Beziehungen der 3 Farben beziehungsweise Paritäten der 4D-Oszillation. Hier als ++; +-; -+; und das resultierende Moment - - (als Weiss im Zentrum der Darstellung). Diese Darstellungsweise ergab sich aus den Versuchsreihen in CERN und der Interpretation von Teilchen und ihren Eigenschaften.
Die Matrix Theorie kennt keine Teilchen, nur schwingende Felder mit koordinierten Oszillationen, dessen Wirkung als Paritäten und nicht als statischen Eigenschaften von Teilchen im (leeren) Raum gesehen werden. Eine Parität schliesst immer auch die Gegenseite der Schwingung ein, wobei das Geheimnis der Antimaterie automatisch gelöst wird.
Um die Rolle der „leeren“ Oktaeder in S1 / S3 als bindende Felder zu verstehen, werden 2 Feldverbände im unteren Bild gezeigt.

Links wird in symbolischer Form der Euklidische Raum der Dichte Null gezeigt. Die Roten Felder (Protonen) bilden mit den blauen Feldern (Antineutronen) ein Verband, der mit den konträren Sekundär-Felder in diskreten Abständen und Bindungen gehalten wird. In den Misch-Feldern, hier Weiß, wird die Matrix in +/- ausgeglichen und damit abgeflacht, was Anziehung bedeutet. Es zeigt die Phase (Parität der Oszillation im S1), wo das Proton die sogenannte Ladung (SM) (+) und das Neutron in der Anti-Neutron Phase die Ladung (-) hat. Die Quadrate symbolisieren die Oktaeder eines Layer‘s. Die Pfeile zeigen die Bindungsrichtung. Die Kreuz-Richtung symbolisiert die Z-Richtung zum nächsten Layer. Die Überschneidungen bilden sich in S3. Dieser hier nur exemplarisch gezeigte Verbund würde ein Materie-Stadium zeigen, dass praktisch unglaublich hart und schwer wäre. Es könnte das Material eines Schwarzen Loches sein, denn Singularität gibt es nicht in der Physik, nur in der Religion. Vielleicht werden wir eines Tages Vorgänge im Zentrum unserer Galaxie entdecken, die mit diesem 5. Aggregats-Zustand erklärbar würden.
Rechts sehen wir das gleiche Bild, jedoch relativistisch verzerrt. Protonen und Antineutronen werden stark reduziert. Die weißen Felder zeigen den Bindungs-Effekt. Zu beachten ist, dass das rechte Bild als Ganzes kleiner ist. Dies sollte als Link zur Gravitation gedeutet werden.
Der β-Zerfall
Hier soll nun eine Transformation des β-Zerfalls mit den Feld-Relationen der Matrix erklärt werden. Dabei gilt eine Sicht aus der 4. Dimension, wo unser 3D-Raum zur Oberfläche im 4D-Raum wird. Es wird angenommen, dass die Vertikale die 4. Dimension und die Horizontale den 3D-Raum symbolisiert. Weiter wird angenommen, dass die Oszillationen nur aus der Sicht der Oberseite als (+) gesehen wird. Ein Proton ist hier ein Ausschlag nach oben, es ist die (+) Parität des Protons als Referenz. Als Oszillation können jedoch alle Darstellungen auch horizontal gespiegelt dargestellt werden.

Das nebenstehende Bild zeigt schematisch die Hierarchie der Elementar-Teilchen in der Maßstabs-Ordnung der Matrix. Zu Oberst das Proton als Impact aus der 4. Dimension S1 mit den Sekundär-Felder S3, S9 und den Anfang des Ladungs-Feldes der Elektronen-Bindung. Rot ist hier die (+) Parität und Blau die (-) Parität.
In der Mitte wird das freie Elektron in gleichen Schemata dargestellt. Es ist der Impact aus der 4. Dimension in S3 , des Sekundär-Feldes S9 und den Anfang des Ladungs-Feldes der Elektronen-Bindung.
Das untere Bild zeigt im gleichen Matrix-Schema eine schwache Einwirkung aus der 4. Dimension in S5 und S7 als (+) und (-), wobei S9 nur mitschwingt und keinen Impuls mehr aus 4D bekommt, da die Einwirkung zu schwach ist. Der Bereich S5-S9 hat daher keine Ladungs-Wirkung und gilt als Gesamtbereich neutral. Er verursacht keinen Moment im Ladungsfeld S9 - S27. S5 – S9 ist der Maßstab der Neutrino’s.
Alle dargestellten Felder bestehen aus einem Impact der 4. Dimension als Primär-Feld und den gebundenen Parafelder bzw. Sekundär-Felder im 3D-Raum. Sie alle haben daher V=<c.
Bei dieser Analyse der Matrix-Schemata kam ein äußerst trivialer Fehler
der Physik des Standard-Modells zu Vorschein. In der Auffassung der Physik
des 19. Jhd. waren Teilchen etwas Festes und Massives. So wurden in Laufe
der Forschung alle ihre festgestellten Verhaltensweisen ihnen als
Eigenschaften zugeordnet. Sie waren nie der Raum selbst bzw. seine
Phänomene. So wurde dem Proton willkürlich die Ladung (+) zugeordnet. Nach
den Erfahrungen im elektrischen und magnetischen Feldbereichen erzeugten die
Eigenschaften (+) und (-) Anziehung. Da Protonen und Elektronen sich
anzogen, wurde das Proton als (+) und das Elektron als (-) gesehen. Die
Matrix sieht das anders. Es sind dort alle Abstoßung und Anziehung
Wechselwirkungen der dem Elementar-Teilchen umgebende Felder. Die
Wechselwirkung Proton-Elektron passiert generell im S27 und bildet dort die
Felder, die „Elektronen-Schalen“ genannnt wurden. Die Wechselwirkung Proton/Elektron im gleichen
Raum-Punkt, ein Zustand des
Neutrons, passieren im Sekundärfeld S3 und erschaffen dort eine sehr
starke Bindung, die wahrscheinlich nur bei der Bildung von Neutronensternen
während einer Supernova erreicht wird. Da die Sekundärfelder zwiebelförmig ein Wechselspiel von +
/ – bzw. ++ / +- haben, ist das Proton das Zentrum von
- (+Proton+) -. Das Elektron als Konter-Oszillation
hätte dann +
(+Elektron+)
+. So hätte das Elektron im Wechselspiel
des gesamten Raumes immer die Konter-Oszillation zum Proton.
Hier kurz erklärt, warum vereinfacht mit +/- gearbeitet werden kann.
Die Paritäten ++/+- sind in der +Zeit und können von uns beobachtet werden. Die Paritäten -+/- - sind für die Oszillation eines ganzen Zykluses im 4D-Raum notwendig, können jedoch experimentell von uns nicht nachgewiesen werden, da sie in der (-) Zeit passieren. Der Grund dafür ist unsere kosmische Situation, wo wir uns in der Zeitlinie (Start-Ziel) zur Zukunft befinden. Würden wir die Zeitlinie umkehren, dann würde die Welt für uns gleich sein, wir würden ++/+- als Antimaterie betrachten und unser Universum würde kleiner werden anstatt sich auszudehnen.
Hier der Beta-Zerfall:
Die Kernphysik interpretierte den Vorgang aus der β-Strahlung. Sie
erkannte, dass sich bei der Kernspaltungs-Energie ein Proton in ein Neutron
verwandeln kann. Da dieser Vorgang die Ordnungszahl des Atoms ändert, wird ein
(β−) Zerfall bei der Ordnungszahl + 1 und ein (β+) Zerfall bei der
Ordnungszahl -1 angenommen. (Physiker neigen zum komplizierten). Der (β−) Zerfall bedeutet
dann, ein Neutron wird zum Proton (Ordnungszahl + 1) und bei (β+) Zerfall,
ein Proton wird zum Neutron (Ordnungszahl -1).
(β−) Zerfall
n -> p + e- + ʋ- =
Neutron n=Neutron, e- = Elektron, ʋ- =Anti-Neutrino
(β+) Zerfall p -> n + e+
+ ʋ+
= Proton e+ = Anti-Elektron (Positron), ʋ+ =Neutrino
Hier zeigt die Raum-Matrix ihr wahres Gesicht. Die Wechselwirkung Proton/Elektron passiert im S3. Dort jedoch ist das Feld in der (-) Parität und das Elektron in der (+) Parität. Hier gelten nur die Paritäten, nicht die Ladung, welche eigendlich nur ein idealisierter Ausdruck einer statischen Beschreibung der Partikel ist, jedoch von der Matrix-Theorie als Paritäten der Oszillationen gesehen werden.
Der (β−) Zerfall
n -> p + e- + ʋ-
Das Proton (im + Feld S1) empfängt ein Elektron in seinem Sekundär-Feld (-
Feld S3) ein Elektron, welches in gleicher Frequenz von S1 dort in S3 ein +
Feld ist. Dadurch neutralisiert sich S3. Das neutralisierte Feld S3 dehnt
den Raum dort wegen der neutralisierten Energie aus (λ=h·c/E), was
das zum Elektron gehörende Sekundärfeld S9 (-Neutrino) abwirft. Es wird
durch die hochenergetische Wechsellwirkung herausgeschleudert. Ebenfalls
wird der Vorgang im S3 Wirkung auf Primärfelder S27 haben, was Photonen
erzeugen würde.
Der (β+) Zerfall würde
im gleichen Sinn mit umgekehrten Paritäten erfolgen.
In der Matrix-Feldtheorie wechselwirken nur Felder des gleichen Maßstabes. Beim Betazerfall wechselwirkt ein Proton daher nur via Sekundär-Feld S3 mit dem Elektron in S3. Wenn dort das Proton die Parität (-) hat, dann würde dort ein Elektron mit Parität (-) abgestoßen. Es gäbe kein Grund für so eine Bindung. Ein freies Neutron hat immerhin eine Lebensdauer ~15 min.

Anders jedoch, wenn die Annahmen der oben gezeigten Bilder gelten. Dort müsste „nur“ die Barriere S9 überwunden werden.
Die Formeln sähen nun so aus: Bild links:
Proton in S1+ ; S3- ; S9+
Elektron in S3+ ; S9-
Neutrinos in S9 sind hier neutraler Raum.
S3+-
hebt sich auf
S9+- hebt sich auf
Es bleibt ein neutrales Proton, neu
nun Neutron genannt.
Teil 4 zeigte die Anwendung der Matrix-Theorie auf die Kern-Physik. Weitere Anwendungen würden zu weiteren Forschungs-Felder führen, was den Rahmen dieser Schrift sprengen würde.
Was wurde erreicht?
Das Konzept eines 4 dimensionalen Raumes zeigt uns einen völlig neuen Feldtyp, der mit seiner Abstraktion als Mehrfach-Feld bezeichnet werden kann, ein Feld aus Feldern, die wiederum aus Feldern bestehen. Dieses Feld erklärt die innere Struktur der Fermionen. Es zeigt die inneren Felder der Fermionen, das Primär-Feld um den punktförmigen Moment im Zentrum als Schwingung der 4. Dimension. Darauf folgt das Primär-Feld des Elektrons, die Felder der Neutrinos, das Ladungsfeld oder auch Feld der Elektronenorbitale, weitere Felder der Chemie und der Spannungen im elektromagnetischen Raum. Die multiblen Felder zeigen ein Konzept, dass auch das kleinste Teilchen als Feld erkennt und dieses Prinzip bis auf die Gravitation ausdehnt. Ein Prinzip, das alle Theorien der Physik vereinen könnte. Grundlage dieser Erklärung ist die Matrix als Geometrie einer 4-dimensionalen Raumstruktur und die quantisierten Schwingungen aller existierenden Dinge, die erst in größerem Maßstab als analoge und statische Manifestationen unserer bekannten Welt erkennbar werden

Weinachten 2016 fing ich an, meine Idee einer Raum-Matrix als Web-Page „Der Feldraum“ zu beschreiben. In den Jahren 2017 und 2018 wuchsen die Ideen im Kopf und in meiner 3D-CAD Plattform zu einem Zoo von Lösungen, die eine logische Ordnung verlangten. Im Juli 2018 fing ich an, diese Ideen in logischer Folge mit Word und Bild zu dokumentieren. Die einzelnen Themen produzierten sich selbst und versetzten mich mit ihren überraschenden Lösungen ins Stauen.Es wuchs ein neues Bild der Physik, nicht erdacht aber gesehen.
Gunter Michaelis, Griesbach, März.2022
Kurzgefasste Papiere ähnlicher Thematik
Das physikalische Medium oszilliert
Die Geometrie des Medium "Raum""
Die Sicht auf das Universum ist eine Illusion
Friedmann-space und die Matrix des Raumes
Das Raum-Zeit-Kontinuum
Die Illusion der Raum-Zeit
Partikel in der Matrix-Struktur
Das Elektron
