Die MATRIX ein neues Konzept des Raumes

Der Tetraeder ist die einfachste 3D-Form. Sie erfüllt die Bedingung, eine Form mit gleichen Distanzen seiner 4 Ecken eine allseitige stabile Konstruktion zu bilden. Um die Distanz zu fixieren, wird ein Maßstab (scale 1) S1 angenommen, der im Moment noch keinen Bezug zu einen physikalischen Wert hat. Weitere geometrische Betrachtungen beziehen sich auf ihn. Den physikalischen Wert dieser Form bilden die 4 Farben an den Ecken. Sie sind als Raum-Orte gedacht, an denen sich 4 Feld-Zentren mit 4 Eigenschaften befinden, die sich in jeder Hinsicht aufheben und nach Außen den Wert Null ergeben, die Bedingung des Leeren Raumes.

Da nach der Planck Formel λ =h•c/E ist, wo λ die Distanz der Feldzentren bildet, haben hier im Maßstab S2 (scale 2) die Zentren die ½ Energie-Werte wie S1. S1 als die Basis aller Betrachtungen hat daher die höchsten Energie-Werte. S2 zeigt aber auch, dass seine Ecken alle die gleiche Farbe haben. Ein gefüllter Raum mit Stabgrößen S2 kann Energien nicht lokal halten, sie breiten sich mit V=c aus. Hier kommen wir zu eines der wichtigsten Eigenschaften des „leeren Raumes“. Es zeigt sich, dass alle ungeraden Maßstäbe sich zum Null-Wert aufheben und alle geraden Maßstäbe wie hier S2 oder S4; S6; S8 usw. eine Maßstabs Schicht ergeben, die als Medium aller darin enthaltenen Kräfte sind. Sie pflanzen sich mit V=c fort bzw. propagieren.

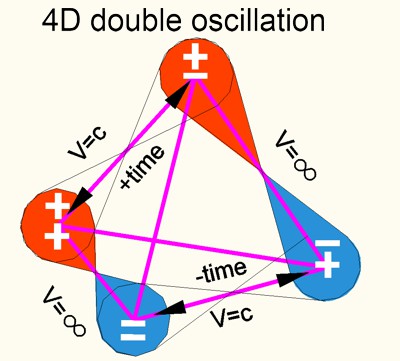
Auch in einer multiplen Anwendung (Füllung ohne Zwischenraum) findet jeder Raumpunkt als Eigenschaft (Farbe) den Ausgleich im Nachbarfeld. Die Raumpunkte schwingen in einer Doppel-Oszillation. Der Zyklus umfasst 4 Zustände des Raum-Kraft-Kontinuums, 2 Zustände der Zeit und 2 Zustände des Raums. Dieser Umstand verführte die Physiker, den Fermionen ein Spin bzw. Helizität (links/rechts) zuzuordnen. Später wird das Thema eingehender behandelt. (siehe das Thema "Der leere Raum Einsteins").

Die Matrix des LEEREN RAUMES zeigt daher in seiner innersten Struktur 2 Eigenschaften; eine, die jede erdenkliche Kraft halten kann (S1;S3;S5 usw.) und eine, die der Matrix als Medium alle Energien unseres Raumes mit V=c sich ausbreiten lässt (S2;S4;S6 usw.).

Bei genauerem Hinsehen entdecken wir, dass im Inneren des Tetraeders S2 ein Oktaeder liegt. Da aber dessen Ecken mit den Feldzentren der Tetraeder gebildet werden, ist der Oktaeder hier nur ein Zwischenraum ohne Inhalt. Seine Größe ist hier S1. Ein Oktaeder S2 wäre sowieso in der Zwischenzone der Ausbreitung und würde daher nur aus Feldzentren gleicher Farbe bestehen, die nicht wie S1 oder S3; S5; S7 usw. ein Werte-Equilibrium bilden können.
Die Größe S3 hat die gleichen Eigenschaften wie S1. Da ihre Stab-Größen 3 mal länger sind als S1, wechselwirken sie nur mit 1/3 der Energie von S1.

Er ist nicht nur ein Zwischenraum, er hat Eigenschaften, die Ihn zum Träger unserer Welt werden lassen. Er ist der Sitz der Materie, während die Tetraeder das Medium sind.
Natürlich bilden Tetraeder und Oktaeder als Raumelemente eine einzige Struktur, die zusammen keinen leeren Raum übrig lässt. Der Raum ist somit vollkommen geometrisch definiert. Pro Raumeinheit befinden sich 2 Oktaeder + 4 Tetraeder. Diese haben ein Volumenverhältnis von 1 zu 2 d.h. 1/3 Volumen Tetraeder und 2/3 Volumen Oktaeder.
Diese Werte aber haben keinen direkten Einfluss auf den Raum.

Eine Berechnung nach Pythagoras (d=√(x^2+y^2+z^2)) hätte bei dieser hexagonalen Raumstruktur der Matrix wenig Sinn, da eine präzise Berechnung nur integer Werte haben kann. Der Raum ist durch die Forderung von zusammenhängenden Maßstäben quantisiert. Nebenstehend ist ein Tetraeder mit kolorierten Abständen dargestellt. Der im Zentrum liegende Oktaeder wurde mit leicht transparenten Flächen bezogen. Die an den Dreiecksflächen angebundenen Tetraeder stellen hier die Raumeigenschaft eines Mediums dar. Hier werden die Kräfte der Raumstörungen mit V=c weiter geleitet. In diesem Fall hättet der sich so ergebene Tetraeder die Größe S6. Der Oktaeder hat die Größe S3.

Was ist das Spezielle beim Oktaeder?

Sind die umgebenden Tetraeder ausgeglichen, dann ist der Oktaeder leer. Sind die Tetraeder unausgeglichen, dann entsteht aus der Fehl-Farbe im Zentrum des Oktaeders ein Moment aus der 4. fehlenden Farbe seiner Umgebung. Die Diagonalen werden als Farbe von den Nachbar-Oktaedern übernommen und bilden einen fortlaufenden orthogonalen Raum. So können große Räume Momente erhalten und Kraft-Bereiche der Fehlfarben erzeugen. Dieser orthogonale Raum wird stabilisiert von der Flankierung eines jeden Oktaeders mit der doppelten Anzahl Tetraeder.

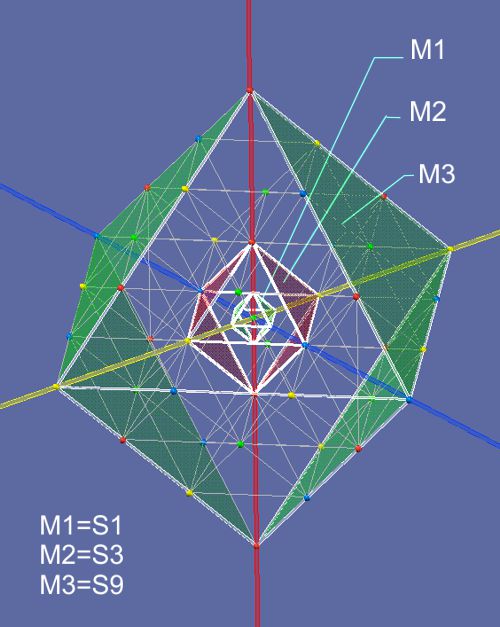Die Störung größerer Bereiche des Raumes im gleichen Maßstab erzeugen die Zentren in den Oktaeder, welche einen elastischen Widerstand erzeugen wodurch sich Kraftfelder ergeben. Diese manifestieren sich zwiebelförmig um einander im Längenverhältnis ihrer Stäbe wie 1; 3; 9: 27; 71 usw. bzw. λ=3^x oder 3^(-x). Somit ergeben die Oktaeder eine weitere Eigenschaft des Raumes neben der obengenannten Eigenschaft einer zwiebelförmigen Schichtung von Kraft haltenden Bereichen ungerader Maßstäben und Kraft emittierender Bereiche gerader Maßstäbe.

Geometrische Daten

Der Oktaeder wird durch 8 Seiten bestehend aus 12 gleich langen Kanten und 3 Diagonalen gekennzeichnet. Er ist die verbindende Form für 6 Ecken, die als Zentrum für 6 Sphären in 3 Farben stehen. Seine Ecken berühren eine übergeordnete Späre mit den Radius r=√1/2=0.794. Trotz der recht harmonischen Werte hat er kein Äquilibrium seiner Farbwerte. Als Bestandteil eines neutralen transparenten Mediums und Träger höchster Energien darf er keine Momente (Farben) an seinen Ecken haben. Wie in den oberen Bildern zu erkennen ist, sind die hier gezeigten Farbmomente = Null. Sie gehören energetisch zu den ihn umgebenden Tetraedern. Der Okteeder ist ein reiner Zwischenraum. Trotzdem hat er die Raumdichte der Entropie seines Standortes. Wenn diese ändert, dann wird ein Farb-Moment in seinem Zentrum erzeugt. Wir werden bald sehen, dass ein Oktaeder weniger stabil als ein Tetraeder ist.

Eine abrupte Störung der lokalen Entropie (Experimente in LHC Genf) hat hauptsächlich Wirkung in seinem Zentrum, in dem das fehlende 4. Farbmoment, die "Manko-Farbe" erscheint. Diese Mankofarbe wird von dem im nächst höheren Massstab wirkenden Farbmomenten erzeugt, hier Grün im Massstab S2, wenn vom Massstab S1 für den Oktaeder ausgegangen wird. Auf jede Fläche (Dreieck) des Oktaeders steht ein Tetraeder. Es sind daher 8 Tetraeder, die in sich mit den Farbmomenten des Oktaeders und ihrer Spitze die 4 Farbmomente des Äquilibriums haben. Es entsteht eine Raumstruktur, die nebst der Steifheit der Tetraeder in ihren Zwischenräumen in Form von Oktaeder eine elastische Ausgleichszone hat.

Hier kurz die geometrische Konstruktion der inneren Abstände eines Tetraeders. Wir erkennen 6 Kanten (3 grüne und 3 weisse, die optisch zum Oktaeder gehören). Wir sehen im weissen Dreieck (Basis) die Konstruktion seines Flächenzentrums. Von dort (rechtwinklig) liegt die vertikale Achse. Der Kreuzpunkt einer rechtwinklig gezogene Linie von der Mitte einer Kante ergibt das Volumenzentrum des Tetraeders. Von dort können 4 (rote) Linien zu den Ecken laufen, die dann den Radius einer Sphäre bilden, die alle 4 Ecken des Tetraeders berührt. Der Radius dieser Sphäre wäre bei der Seitenlänge=1 dann 0.617. Dies zeigt, dass ein Tetraeder stabiler als ein Oktaeder ist (Radius vom Volumenschwerpunkt zu den Ecken = √(1/2)=0.707), das bedeutet (< r=>E(E=hc/λ)). Zudem ist die quadratische Grundform des Oktaeders leicht verformbar, die Kräfte (und damit die Stabilität) werden dann über den steiferen Tetraedern geleitet. Die Verformung des Raumes geht also über die Verformung der Oktaeder. Weitere Details in: Geometrische Analyse der Matrix

Unser Universum als Beweis der 4. Raumdimension

Unser Universum wird sich normaler Weise als eine expandierende Kugel vorgestellt. Die Kugelform kommt von unserer Sichtweise, die auf allen x;y;z Richtungen gleich weit 13.6 Mia Lichtjahre aufzeigt. Die Ausdehnung kommt von der Hubble Konstante, die besagt, dass alle beobachtbaren Teile unseres Universums sich je nach Distanz voneinander entfernen. Das heißt ca. 70 km/s pro Mpsc (Megaparsec). Anders ausgedrückt: 2.2 km/s pro 100´000 LJ. Alle 100´000 Lichtjahre nimmt also die Geschwindigkeit der Ausdehnung zu. Wenn sie in 13.6 Mia LJ alle 100´000 LJ 2.2 km/s zunimmt, dann hat sie am Ende Lichtgeschwindigkeit.

13.6 10^9/10^5 * 2.2km/s = 13.6 10^4 * 2.2 km/s = 299 200 km/s

Wenn der BB (Big Bang) bzw. der AA (Aller Anfang) sich von uns mit V=c wegbewegt, dann bedeutet dies für uns, nicht der AA sondern wir sind die, die V=c haben. Das aber entspricht nicht der SR (spez. Relativität) und der GR (Generellen Relativität). Diese sagen, dass die radiale Koordinate dieser Ausdehnung bei V=c nur Null und unendliche Werte bekommen würde. Wir wären praktisch nur noch 2-dimensional. Das jedoch ist falsch.

Die Lösung bietet der Einbezug der 4. Raumdimension. Aus der Sicht der 4. Raumdimension würde unserer Raum eine sphärisch gekrümmte Fläche sein (der gekrümmte Raum Einsteins), die sich als eine Impulswelle mit V=c im 4D Hyperraum ausbreitet. Alle 3 Raumkoordinaten unseres 3D-Raumes würden im Normal-Modus bleiben, die 4D-Koordinate wäre jedoch dann als Tensor (rechtwinklig zu den 3D-Koordinaten) für uns unsichtbar. Eine sekundäre Wirkung wären hier die subatomaren Partikel, die in 4D eine Strahlung mit V=c, im 3D jedoch eine locale Wirkung V<c wären.

Es ist zu erwähnen, dass Marco Pereira, MSc in Physics, PhD in Physical-Chemistry , auf dieser Idee eines im Hyperraum sich mit V=c ausdehnendes Universums seine weit umfassende Theorie eines Hypergeometrischen Universums (HU) aufbaute. Ich schrieb die erste Page der Matrix Theorie 2016 ins WWW. Die HU Theorie sah ich als weitgehende Bestätigung. Es war jedoch Billy Lee, Freidenker, der mich auf den Hubble Effekt von V=c bezogen auf die Grösse (13.6 Mia LJ) unseres Universums aufmerksam machte.

Wie wir später sehen werden, ist ein Hyperraum als Basis und Träger unserer 3D Welt unbedingt notwendig. Seine Konsequenzen im Kontext unserer Weltentstehung werden jedoch hier nicht erörtert. Hier soll die Existenz des Hyperraumes als ein wichtiger Bestandteil der Matrix Theorie dargestellt werden. Er hat 4 Koordinaten, die Zeit wird nicht dazu gezählt. Zeit wäre hier nur der Effekt einer Oszillation und keine räumliche Dimension. Die relativistische Gleichung Null=(ct)^2-x^2-y^2-z^2 bedeutet  => ct (eine Distanz in V=c) = √x^2+y^2+z^2 also ein Vektor im 3D-Raum. ct ist hier nicht die 4D-Koordinate, Zeit jedoch ist hier nur ein von uns erkennbarer Effekt. Erst aus der Sicht der 4. Dimension wird erkannt, dass das Universum, d.h. ganze Koordinations-System um ct weiter bewegt hat. Das Universum ist während der Distanz d=√x^2+y^2+z^2 um ct mal Radius grösser geworden.

Ein guter Beweis für das Paradox unserer Sichtweise ist der Fakt, dass von uns aus alle Distanzen in die Vergangenheit zeigen, da wo die Galaxien dichter werden bis hin zum CMB (Cosmic Mikrowave Background), hinter dem sich 0.0003% der Distanz der Urknall befindet. Und das in allen 360° mal 360° Richtungen. Konsequenz: Wir sind im Mittelpunkt des Urknalls. Lösung: Der Urknall lieg im Mittelpunkt einer 4D-Sphäre, deren Oberfläche unser gekrümmter Raum ist. Daher ist alles in unseren Universum gleichweit vom Urknall entfernt.

Einstein benutzte die Zeit als gleichwertige Raum-Koordinate, um so seine Math für einen V=c abhängigen Raum zu beschreiben. Dies bleibt bestehen, wenn es um den von uns sichtbaren Raum geht. Die Zeit wird in der Matrix Theorie als eine Zeit mit (+) und (-) Werten ergänzt, da es hier nicht um das Universum, sondern um die Quanten-Dynamic der Partikel geht. Dort zeigt sich die Zeit zyklusgebunden und getrennt von der Zeit des Universums. Einen universellen Zyklus der Zeit ist jedoch anzunehmen und entspräche der Philosophie einer vollkommenen Harmonie.

Der euklidische, der sphärische, der relativistische Raum

Natürlich gibt es noch Raum-Konzepte. Sie alle kämpfen mit der Darstellung auf das übliche 2-dimensionale Papier. Im Prinzip können alle 3 Arten der oben genannten Konzepte polydimensional sein. Mathematisch gesehen ist der Euklidische Raum ein Konzept, das unser normales Verständnis des Raumes entspricht. Andere Raum-Konzepte können daher auch euklidisch dargestellt werden. Zu der Beschreibung eines Raumes gehören jedoch auch Distanzen, Flächen, Volumen und n-dimensionale Werte. Diese jedoch sind bei den verschiedenen Konzepten nicht mehr gleich.

Der Euklidische Raum

Dieses Raumkonzept geht von einer isotropischen Verteilung seiner Einheits-Größen aus, die unendlich kleine Raumeinheiten sind. Sie sind analoge Größen, d.h. sie können beliebig unterteilt werden. Die Distanzen errechnen sich mit d=√a^2+b^2+n^2 wobei n für die Koordinaten weiterer Dimensionen steht. In dieser Weise können Kugeln, Kegel, Konus usw. berechnet werden. Für die weitaus meisten Fälle ist diese Berechnungsart genügend.

Der sphärische Raum

Obwohl jede Sphäre, d.h. ein Kreis, eine Kugeloberfläche, ein Kugelvolumen usw. auch euklidisch berechenbar ist, sind die Ergebnisse im sphärischen Raum anders. Seine Koordinaten sind alle mit π gekrümmt. Allein dadurch ergeben sich Einheiten verschiedener Größen. Durch seine Koordinaten-Krümmung werden sie zu Kreisen, Kugeloberflächen und gekrümmten n-dimensionalen Räumen mit nicht endenden in sich geschlossenen Koordinatenlängen. Der sphärische Raum demonstriert so auf einfacher Weise einen unendlichen Raum endlicher Größe, wie es aus heutiger Sicht von der Größe des Universums erwartet wird. Hier nun eine Formel-Übersicht, die den Einfluss des sphärischen Raumkonzeptes bei den verschiedenen Dimensionen zeigt. Die Bezeichnung D1, D2 usw. gilt für den Euklidischen Raum mit 1, 2, usw. Dimensionen. D1/2, D2/3 usw. gilt für eine Messung im sphärischen Raum mit 1, 2, usw. Dimensionen, der seinerseits in einem euklidischen Raum mit einer zusätzlichen Dimension (Dn+1) eingebettet ist. Ein denkendes Wesen im sphärischen Raum Dn/Dn+1 sieht die Krümmung nicht, sondern erkennt daher diese nur indirekt durch das Ergebnis seiner Messungen.

Die logische Formel-Entwicklung wäre hier d1=Durchmesser; d2=als Umpfang gekrümmt; a1=Kreisfläche; a2=als Kugel gekrümmter Kreis; v1= Kugelvolumen; v2 das gekrümmte Kugelvolumen; w1=der sphärische 4 dimensionale (4D) Raum; w2=der gekrümmte 4D Raum oder die 4D-Oberfläche im 5D-Raum.

Bei der Berechnung des Volumens unseres Universums geht es um den gekrümmten Raum (D3/4). Obwohl vom physischen Standpunkt eine Krümmung im Sinne π als idealisiert gilt, gibt uns die Formeln eine grosse Annäherung an die realen Werte, die, wie wir im Folgendem sehen werden, erst bei der Bestimmung des Mess-Ortes ausserhalb des speziellen Raum-Konzeptes real werden. Krümmungen der dimensionalen Geometrie können nie in der eigenen Dimension gesehen werden.

Wie können sich mehr-dimensionale Geometrien aus einer höheren Dimension vorgestellt werden?

Wir Menschen sind in der glücklichen Lage, 3 Dimensionen in 5 logischen Ableitungen des sphärischen Raumes uns vorzustellen. Diese 5 Ableitungen als 5 Bilder haben eine logische Abhängikeit, die Ableitung sphärischer Grössen. Es sind 5 Vorstellungsbilder, die wir über weitere Dimensionen schieben können, wodurch die Beziehungen der sphärischen Grössen auch in höheren Dimensionen sichtbar werden. Hier ein Beispiel:

Wir betrachten den 4D-Raum in der 4. Dimension. Die Formel 1/2·r^4·π^2 ist in der Kolonne der soliden Kugel. Der gebogene Raum ist in der Kolonne der Kugeloberfläche, der 3D-Raum ist ein gefüllter Kreis, seine Oberfläche ein Kreis und ein gefüllter Kreis wäre dann ein String.

Eine solide Kugel als 4D-Raum mit einem Zentrum (BB) hätte dann den gekrümmten (unseren) Raum als Oberfläche, die wiederum ohne Zentrum und ohne Grenzen wäre.
Genau diese Vorstellung passt auf die Situation unserer Forschung über unser Universums.

Der relativistische Raum

Während der euklidische Raum isotrop ist und gleiche Einheiten hat, der sphärische Raum mit π gekrümmte Koordinaten hat, besteht der relativistische Raum aus der EV (Eigengeschwindigkeit) und der RV (Restgeschwindikeit zu c-V). Das Problem ist jedoch, dass die EV absolut nicht feststellbar ist. Wenn jemand behauptet, dass er eine EV=90% c (Lichtgeschwingigkeit) hat, ist das seine eigene Wahl, jede andere Wahl (z.B. 10% c) wäre ebenfalls wahr. Die RV multipliziert mit der Loretz Metrik ergäbe in beiden Fällen c. Um was handelt es sich bei der Lorentz-Metrik? Im Kapitel "Raum" wurde die Lorentz Transformation erwähnt. Der Mathematiker Lorentz entwickelte auf Gund der Tatsache, dass trotz signifkanter Eigengeschwindigkeit (EV) beim Versuch die Lichtgeschwindigkeit zu messen, nach vorn und nach hinten immer die gleiche V=c resultierte. Dies erreichte er mit seiner der EV angepassten Metrik. Hier ein Beispiel (bei c=1 und EV=90%c) => ϒ''=1/ϒ): ϒ'' (Lorentz-Metrik) =
√(1-(EV/c)²) = √(1-(0.9/1)²) = √(1-0.81) = √0.19 = 0.435 . Die Lorentz Metrik ϒ'' ist hier 0.435.
c=√(EV²+ϒ''²)=√(0.81+0.19) =1, wobei ja 1 als c angenommen wurde. Das gleiche gilt für jede EV.
Klartext: Von jeder EV wird ein Lichtstrahl nach hinten und nach vorn immer als c gemessen!!!

Links:

Das Bild zeigt die Überlegungen von Lorentz im geometrischen Kontext. Basis ist das Pythagoras Dreieck mit c als Hypotenuse, EV und und ϒ'' als Katheten. Die oberen Werte können mit c²=ϒ''²+EV² errechnet werden.
Darunter das gleiche im Kontext zu Flächen.
Hier wird gezeigt, dass es nur eine absolute Geschwindigkeit gibt, die des Lichtes. Da wir und unsere Mess-Geräte aus Oszillationen mit V=c bestehen, bleiben wir relativ. Unsere wahre Geschwindigkeit bleibt für uns ein Geheimnis. Wir können niemals unsere EV oder die wahre RV (Restgeschwindigkeit) wissen. Wir würden es nicht merken, wenn wir mit EV=90%c durch den  Raum rasen würden. Es ist die Metrik des Lorentz-Faktors, der mit seiner Metrik jede Geschwindigkeit mit der Rest-Geschwingigkeit zu c addiert. Das gilt für alle Dimensionen, die das Medium "Raum" zu seiner Definition benötigen. Wir sehen hier, dass es in der speziellen Relativitätstheorie nur für einen Vektor (String-Grösse) und seiner Zeitrichtung anwendbar ist, in der allgemeinen Relativitätstheorie gilt das auch für die Raumdichte. Da die von EV/c abhängigen Koordinaten-Werte eine unterschiedliche Metrik schaffen, können natürlich auch ganze Raumfelder aus kleineren oder grösseren Einheiten bestehen, die dann als Raumdichte definiert werden können. Der relativistische Raum ist daher nie isotrop. 
Um die Lichtgeschwindigkeit zu messen, ergibt sich für jede Geschwindigkeitsdifferenz c-V das Ergebnis c, da c die Geschwindigkeit der Elastizität des Mediums ist. Nach der Matrixtheorie ist der Raum mit seiner inneren Struktur das Medium , wobei die kleinere Struktur das Medium der größeren ist. Die Größere aber ist die Struktur der Materie.
Daher ist Materie verdichteter Raum, ein Raum im Raum.

Die wahre Natur einer universalen MATRIX

Die bisherige Erklärung der Matrix als eine Raumstruktur lässt das Gefühl aufkommen, dass trotz raffinierter Geometrie und auffälliger Kompatibilität mit moderner Quantendynamik sie eine willkürliche Struktur in den uns nicht zugänglichen Bereichen und Maßstäben der Physik zu sein scheint. Im Kapitel Unser Universum, der Beweis der 4. Raumdimension wird ein Szenario einer Weltentstehung aufgezeigt, die auf Fakten einer Jahrhundert langer Beobachtung des Universums basiert, der Hubble Konstante. Im 4 dimensionalen Hyperraum entsteht eine aus einem Zentrum entstandene sphärische Wellenfront, die mit V=c in den weiteren Hyperraum propagiert. Die hier verbale Darstellung zeigt den Hyperraum als 3D-Raum, dem entsprechend wird unser 3D-Raum als eine Wellenfront (geometrisch also eine Fläche) vorgestellt. Die Ausbreitung im 4D-Raum ergibt im 3D-Raum die Hubble Konstante, also 2.2 Km/s per 10·10^4 LJ. Dies würde auf einer Distanz von 13.6 Mia Lichtjahren V=c ergeben. Wenn V=c als die Medium-Geschwindigkeit gesehen wird, dann ergebe es ein sichtbares Universum von 2·13.6 Mia Lichtjahre als Durchmesser. Aber diese Größe von 27,2 Milliarden LY ist nicht nur eine Entfernung, sondern auch eine Zeit in die Vergangenheit.
Aus unserer Perspektive sehen wir daher am Ende dieser Sphäre eine harte glitzernde Oberfläche, den Anfang von allem, was ist. Wir sehen nicht das Ende des Universums, sondern das Ende der Zeit.

Dies ist nur mit höheren Dimensionen erklärbar, um die es hier ganz sicher geht. Wir müssen aus der 4. Dimension schauen und uns das als eine dreidimensionale Szene vorstellen. Unser Universum wird dann die Oberfläche der 4D-Sphäre. Dann wird der Beginn der Zeit zum Zentrum dieser Sphäre. Das Äußere der Kugel wird zum „Hier und Jetzt“. Wir werdent flach wie "flat earthler", und auf der Oberfläche dieser Sphäre leben. Für uns erscheint das Universum endlos und ohne Zentrum. Aber um die Zeit zu erklären, braucht man ein Zentrum, einen Anfang. Wenn wir diesen Anfang als Urknall (BB) bezeichnen, dann wird dieser jedoch in unserem Raum (der Oberfläche) nicht zu finden sein. Wir sehen ihn nur, wenn wir in die Vergangenheit blicken. Wir sehen den kosmischen Mikrowellen-Hintergrund (CMB) und wissen, dass nur 0,003 % hinter seiner Entfernung zu uns der Urknall liegt.

Wir fragen uns, wie groß die Größe unseres Universums ist. Dies kann mit den dimensionalen Formeln gefunden werden, siehe: Wie kann die Geometrie höherer Dimensionen sich vorgestellt werden. Das Volumen des gebogenen Universums ist in seinem 3D-Volumen (1/2)·(3/2π) = 2.36 *) mal größer. Das ergibt sich aus dem Verhältnis (2π^2·r^3) / (2·(4/3π·r^3)) oder der Gleichung 4D-Kugel / 2·3D-Kugel (siehe Kapitel: Der sphärische Raum).
*) Jede Dimensions-Erhöhung Dn zu Dn/(n+1) verdoppelt zusätzlich zur Biegung die Grösse, da zur (+) Grösse dann auch die (-) Grösse dazu kommt. Z.B. zur Kreisfläche => Kugelfläche ist die Biegung der Kreisfläche nach oben und nach unten. Dabei bekommt auch die Kreisfläche im 3D-Raum eine Ober- und Unterseite. Im Kapitel Hyper-Raum (Materie/Antimaterie) wird das angewandt. Wir können davon ausgehen, dass ein 2.36 größeres Volumen des Universums (v=r^3·4/3π=13.6^3·10^27·4/3·3.14) = 10.535·10^30·2.36 = 24.9·10^30 LJ^3 zu einem Radius von R=√3 ((v·3/(4π)) = 18.1 Milliarden LJ führt.
Das ist jedoch nur der Radius einer Runde im endlosen Universums, es ist nicht der Radius des gekrümmten Raums in der 4. Dimension. Man kann dies so beschreiben: Der Radius eines Volumen einer Sphäre in einem gekrümmten Raum mit r=13.6 Mrd. LJ wird in den gekrümmten Raumlinien als r=18.1 Mrd. LJ gemessen. In einer polydimensionalen Darstellung (wenn die 4. Raum-Dimension als 3D sich vorgestellt wird) muss mit einer Sphäre mit r=18.1 Mrd.LJ gerechnet werden.
Wie viele Dimensionen auch immer  gebraucht werden um komplexe Systeme zu erklären, der anfängliche Radius (13.6 Mrd.LJ) wird sich nie ändern. Die V=c Regel wird nie verletzt.

Hier erscheint etwas schwer nachvollziehbares: In der sphärischen Geometrie ist alles außer dem Anfangsradiusum mit π gebogen. Daher kann der Anfangsradius nur auf den Kreis angewendet werden. Auf der Oberfläche einer Kugel ist der gebogene Radius R=r·π, der Anfangsradius r ist auf der Oberfläche nicht sichtbar. Wird die Oberfläche F=r^2·4·π als Referenz für 2D-Wesen angenommen, dann erkennen diese Wesen den Umpfang/4 oder R=r·π als ihr Radius.
Das linke Bild zeigt die Oberfläche des 4D-Hyperraums, dessen Grösse von uns als 3D Wesen nicht als r (Rot) gesehen wird, sondern als R (der gekrümmte Radius in Gelb). Da dieser R wieder in einem gekrümmten Raum liegt, muss mit r=18.1 Mrd.LJ anstatt 13.6 Mird. LJ angenommen werden. R wäre dann r·π = 18.1 Mia.LJ·3.14=56.9 Mrd.LJ.

Die Größe unseres Universums hätte somit einen Radius R=56.9 Mrd. LJ, was eine Gesamtgröße (Umfang) von 2·π·r = 113.8 Mrd. LJ ergibt. Es hat jedoch aus 4D-Sicht immer noch einen Anfangsradius von 13,6 Milliarden LJ. Die Regel V=c wird nie verletzt.

Was würde das für den Blick durch ein Superteleskop bedeuten? Es könnte in jede Richtung im Raum blicken und den Hinterkopf des Beobachters nach ~114 Milliarden LY sehen. In alle Richtungen! Das ergibt viele Hinterköpfe. Wenn jetzt aber die Zeit und die Hubble-Konstante in die Berechnung einbezogen wird, dann könnten wir die Größe unseres Universums nie sehen, es würde uns schneller entfliehen als V=c. Das ist reine Geometrie; da wird kein Raum extra erzeugt. Die Rosinen-Kuchen-Theorie ist nur ein Kindermärchen. Weitere Überlegungen bleiben dem Leser überlassen.

Sinn dieser Betrachtung ist, die tiefe Natur der 4dimensionalen-Geometrie zu verstehen. Jeder Moment aus dem Vektor der 4. Dimension ergäbe in 3D eine Punktgröße. Diese hätte eine lokale Disposition im 3D-Raum. Erst von hier ergäbe diese Größe lokale, stehende Wellen im 3D-Raum. Dadurch dass so ein Moment während seiner Propagation durch den 4D-Raum (mit V=c) oszilliert, werden die stehenden Wellen zu scheinbar starren statisch stehenden Feldern.

Diese lokalen Raum-Punkte als Oszillation und umgeben von ihren Feldern übernehmen als Momente das geometrische Raummuster des 4D-Raumes und übertragen es 1:1 in den 3D-Raum. Ihre Propagation in der 4D-Struktur wirkt sich im 3D-Raum als Zeit-Zyklus aus und schafft so die 4 Wirkungsarten im 3D-Raum (++) (+-) (-+) (--). Sie und die Struktur des 4D-Raumes sind die Basis-Elemente der MATRIX.