Die Matrix der Elektronen im Ladungsfeld
Eine geometrische Ortsbestimmung der Elektronen ohne Wahrscheinlichkeit
 Das
Neon-Atom
Das
Neon-Atom
Abstrakt:
Das Papier beschreibt die Elementarladung als ein geometrisches Konzept auf der Basis der Matrix-Theorie. Es gibt keine Schalen, Elektronenbahnen oder Orbitals. Es basiert auf der generell starren jedoch verbiegungsfähigen skalierten Struktur der Matrix, dessen Medium grundsätzlich keine Bewegung zulässt. Anstatt dessen wird das Konzept der Propagation benutzt. Wie schon Bohr bemerkte, scheint es, dass ein Partikel bei der Bewegung von A nach B den Raum dazwischen nicht benutzt.
Paradigmen:
Raum
Die Matrix-Theorie sieht den Raum als polydimensional an, wobei 3 Dimensionen den traditionellen Raum und die 4. Dimension als Zeit gesehen wird. Zeit aber ist ein menschlicher Erfahrungs-Wert und gilt nicht im subatomaren Bereich. Dort wird Zeit als eine geometrische Größe der Welllenlänge, der Tensor-Wert einer Oszillation mit Vektor zur 4. Dimension gesehen. Nur so kann das Phänomen der stehenden Wellen erklärt werden, welches hier als physische Existenzform der subatomaren Teilchen gilt. Dieser Raumbereich oszilliert mit den Paritäten der Raum-Dichte, die (unter Einfluss des Lorentz-Faktors) eine Frequenz ihrer ʎ-Werte bzw. Wellenlänge im 3D und 4D-Raum (4-dimensionalen Raum) erzeugt.
Oszillation
Der Matrix-Raum basiert auf der Idee, dass alle Raumteile und Zellen Oszillationen sind. Der Raum ist Oszillation. Seine Bestandteile wie Protonen, Elektronen, Neutrinos, Bosonen und Photonen sind daher Oszillationen mit V=c. Da bei den sehr kleinen ʎ-Werten (Wellenlängen) sehr große Frequenzen entstehen, ist diese Oszillation in unseren Maßstab nicht nachweisbar. Da diese subatomaren Teilchen signifikante relative Differenzen ihrer ʎ-Werte haben, erscheinen die Paritäten der Oszillation als innere Eigenschaften (Ladung, Chiralität, Helizität), der als feste Teilchen gesehenen oszillierenden Felder.
Ladung
Der willkürliche Begriff der Ladung wird in der Matrix-Theorie als das Ergebnis (Parität) der inneren Oszillation erklärt => Ladung. Ein Unterschied des Paritäts-Wertes (Ladung) entsteht dadurch, dass z.B. ein Proton zeitgleich wie ein Elektron entsteht. Unter der Bedingung, dass nur Felder gleicher Größe wechselwirken, hat das Feld des Protons erst dann die Größe des Elektrons, wenn seine Parität geändert hat. Wenn das Proton auf (+) steht, dann hat sein Sekundärfeld (-) und wechselwirkt mit dem gleich großen (+) Feld des Elektrons. Da die Oszillationen im Raum selber begründet sind, hat ein Elektron immer und überall im Raum den Gegenwert des Protons. Da die Frequenz der Oszillation höher liegt als ihre Nachweisbarkeit, sehen wir im praktischen Experiment die Ladung als Eigenwert der Teilchen und nicht als Parität ihrer Oszillation.
Bild 2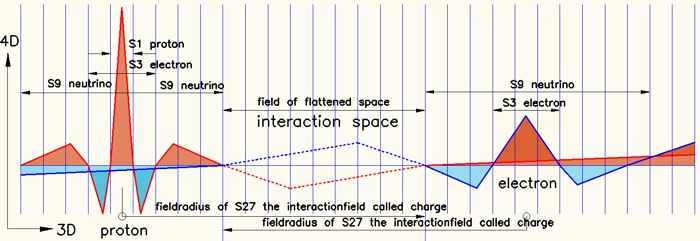
Der Begriff Anziehung oder Abstoßung wird mit der unterschiedlichen Raumdichte zweier Bereiche erklärt, die durch den Ausgleich des Raumes dieses Phänomen erzeugt
Die Geometrie der Raum-Matrix
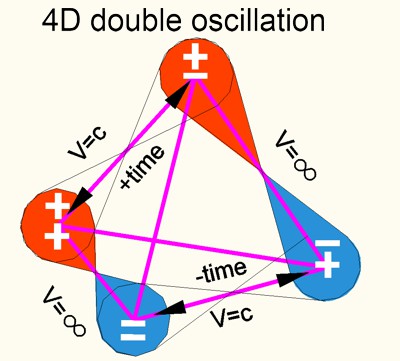 Bild
3
Bild
3
Die Oszillation zur 4. Raumdimension (4D-Oszillation) erzeugt im 3D-Raum ein punktförmiges Primär-Feld, das mit den Sekundärfeldern durch ihre Oszillation verbunden ist. Dadurch entsteht ein Feld mit V<c, auch als stehende Welle oder Soliton bezeichnet, das aus 2 Oszillationen besteht; eine entlang der 4D-Koordinate und eine in die 3D-Koordinaten. Beide Oszillationen sind eindimensionale String-Werte. Die 3D-Oszillation ist ein String mit der Freiheit von 3 Koordinaten während die 4D-Oszillation nur auf eine Koordinate begrenzt ist. Dies gilt eigentlich als ein guter Beweis des kosmischen Konzeptes eines mit V=c expandierenden 4-dimensionalen Universums, wie das von Marco Pereira, MSc in Physics, PhD in Physical-Chemistry in seiner HU-Theorie beschrieben ist. Diese 4 Paritäten der Doppeloszillation bilden in logischer Folge den Tetraeder-Raum, der in meiner Theorie die Geometrie der Matrix als Basiselement des Raumes erklärt wird.
Anziehung und Abstoßung im Feld Raum
Die 4 Dimensionen des Raumes lassen eine (nicht sichtbare) Biegung der Koordinaten im 3D-Raum zu, die als Lorentz-Faktor mathematisch nachweisbar wird. Eine Signifikanz dieser Biegung ist jedoch nur im kosmischen oder subatomaren Maßstab erkennbar. Während im kosmischen Maßstab es als Gravitation erkannt wird, ist es im subatomaren Maßstab die generelle Anziehung aller Teilchen. Da die Biegung des Raumes dort sehr groß sein kann, ergibt es eine Wechselwirkung mit der Entropie (allgemeine Dichte) des Raumes, wodurch die +/- Wechselwirkung (Annullierung) die Raumdichte (Spannung) reduziert wird; Wechselwirkung
 Bild
4
Bild
4
Das Bild zeigt systematisch den verdichteten und den abgeflachten Raum
als Ursache von Abstossung und Anziehung. Die Entropie verursacht eine
Bewegung zum abgeflachten Raum.
Alle Kräfte der Anziehung und Abstoßung
können als eine Wiederherstellung der Balance der Raumdichte interpretiert
werden. In der Matrix Theorie gibt es keine willkürliche Zuweisung von
Eigenschaften wie Ladung oder Gravitation ohne geometrische Erklärung der
Balance.
Feldgrößen
Alle Feldgrößen haben diskrete gequantelte Werte.
Die im 3D-Raum
unterliegen dem Gesetz λ=h·c/E
und die des 4D-Raumes λC = h/(c·m) (
λC=Compton Wellenlänge)
Dabei ist E=Energie, h=Planck hilfsgrösse,
m=Masse und c=Lichtgeschwindigkeit.
Wenn der 4D-Impact für das Proton im
Matrix-Raum auf die Größe 1 gesetzt wird, hat das Elektron die geometrische
Bezugsgröße 1/3, das Neutrino 1/9 und das anschließende Feld der
Elektronen-Wechselwirkung (Ladungsfeld oder Atomhülle genannt) die Größe
1/27. Da aber in diesen Maßstäben die Raumkrümmung eine signifikante Größe
ist, sind die Abstände entsprechend ihrer Energie (Ruhemasse) stark
verzerrt. Die Compton Wellenlänge zeigt die wahren Größenverhältnisse.
λC
= h / (c · m0).
Elektron : λC,e = 2,426 × 10^-12 m E=0.511 MeV
Proton
: λC,p = 1,321 × 10^-15 m E=938,3 MeV
Neutron : λC,n = 1,319 × 10^-15 m E=939,6 MeV
Generell gilt hier die Geometrie der Matrix, die eine Richtgröße ist.
Durch den Einfluss des elektrischen Effektes (λ=hc/E) halten die Seiten
(Stablängen) der Matrix einen bestimmten Energiebetrag. Ist dessen
Energie-Differenz mehr als ein Quant, kollabierten diese in einen kleineren
Maßstab wie S4 zu S3 usw. In der Regel aber haben die Feldgrößen ebenfalls
eine bestimmte Bedeutung wie zB: Neutrino als S5 oder Neutrino als S7 oder
Neutrino S9 für Oktaeder. Die Kernphysik zeigt uns Neutrino S5 und S7 als +
und – wertige Felder zusammen. S9 hat keine Masse mehr. Das Neutrino braucht
jedoch in der Matrix den ganzen Bereich S5 – S9. Damit lässt sich die
Neutralität des Neutrinos mit der Geschwindigkeit V=c der Photonen erklären.
Einen anderen
Einfluss auf die Stablänge hat der Lorentz Faktor, wenn Masse oder
potentielle Energie (eV) involviert ist. Der Richtwert der Matrix z.B.
zwischen Elektron und Neutrino (S3 / S5-9) ist 1/3. Der Wert der Ruhemassen
bzw. Potentiellen Energien ist e=511 eV / n=0.8 eV = ~639 größer. Die
Differenz zwischen der dem Richtwert und des Energiewertes = 639/3=213. Die
Anwendung der Lorentz-Wert-Verkürzung müsste auf dem Diagramm eine Kurve mit
einer Steilheit von 1/213 aufzeigen. Durch diese Verkürzung von
1/213=0.0047 würde die Neutrino-Stablänge in das Sekundärfeld des Elektrons
hineinpassen, wie in der Richtwerte-Matrix verlangt. Die ganze Scene muss
sich so vorgestellt werden, als wenn die potentiellen E-Werte (Masse) die
Steilheit von Gebirgen sind und alles vom Satellit aus gesehen wird.
Wechselwirkung der Ladungsfelder
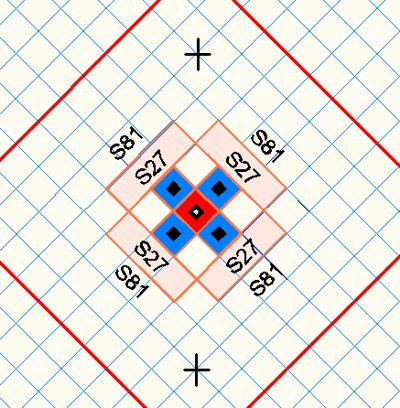 Bild 5.1
Bild 5.1
Mit der geometrischen Strukturierung des Raumes in Tetraeder wird dieser in gleichen Abständen (Stablängen) unterteilt. Bei unterschiedlichen Kräften werden unterschiedliche Maßstäbe erzeugt. Diese werden in meiner Page Matrix: Felder der elektrischen Ladung im Detail erklärt.
Das Bild zeigt ein Proton im roten Feld S9. Daran angedockt 4 Elektronenfelder S9 als Überschneidung der Hyperfelder S27 im Feldraum S81.
Hier ergibt sich ein wichtiger Unterschied zwischen der Matrix Theorie und der anerkannten Physik. Die Ladungsfelder als Sekundärfelder der Elektronen nehmen nicht das Ladungsfeld des Protons ein, d.h. sind nicht das Feld der Elektronenbahnen, sie haben nicht den Atomkern als Mittelpunkt, sondern binden sich an das Feld S9 (in der Feldüberlappung S27) an. Dadurch bleiben die inneren Felder des Elektrons außerhalb der Wirkung der inneren Proton-Felder, wo sie sonst Neutronen bilden würden. Dieser Fall (Neutronenstern) tritt nur unter höchsten Gravitations-Einfluss ein, wo die hohen Energie-Wände (Paulis Exclusion) als eine Barriere kollabieren.
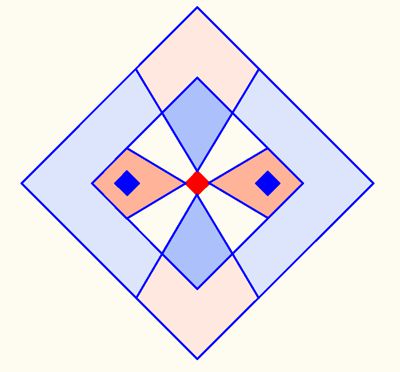 Bild 5.2
Bild 5.2
Innerhalb des Bereiches S 27 und S 81 sind die Matrix-Abstände theoretisch gleich. Da im subatomaren Bereich die Biegungskräfte des Raumes (wegen seiner hohen Dichte) signifikant sind, werden die Matrix-Richt-Abstände stark verformt. Die Geometrie der Matrix ist dort nur ein Eich-Wert. Nach S 27 aber sind Raumverformungen durch die Gravitation kaum mehr erkennbar. Die Matrix als Richtwert zeigt jedoch die Beziehungen der privilegierten Plätze der Elektronen, die mit ihrem eigenen Feld S 27 mit dem des Protons S 27 wechselwirken und sich teilweise aufheben. Die Bindungsenergien (Ionisierungsenergien) werden mit der Wechselwirkung addiert oder subtrahiert und ändern so (λ=h﮲c/E) ihre Feldgrößen. Sie werden dabei durch die elektromagnetischen Kräfte stark verformt. Dieser Vorgang ist sehr komplex und macht die Erklärung durch Ionisierungsenergien nur in Sonderfällen möglich.
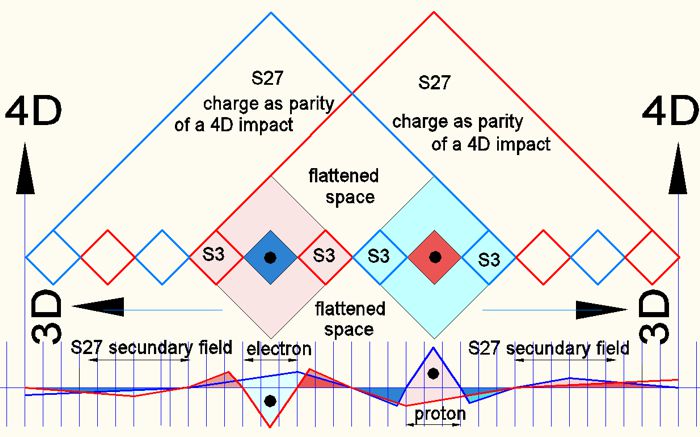 Bild 5.3
Bild 5.3
Das Bild zeigt die Wechselwirkung bei der Überlappung der Feldbereiche S27 im Sekundärfeld S81. Der obere Teil des Bildes zeigt die Überlappung im 3D-Grundriss. Der Untere Teil zeigt die Feld-Überlappung mit der 4D-Koordiate (Energie-Dichte). Im oberen Teil (Mitte) wird der Wechsel der Paritäten in der Matrix des Mediums nachgewiesen. Es muss immer bewusst bleiben, dass die Felder sich im Paritäts-Rhythmus der Matrix (entweder in (++)/(- -) oder in (+-)/(-+) befinden. Das 1. Zeichen (++) ist hier die 4D-Parität und das 2. Zeichen (++) die 3D Parität.Das was als der physikalische Teil unserer 3D-Welt bezeichnet wird, sind Felder, die durch 4D-Einfluss in den 3D-Begrenzungen der Matrix entstehen.
Es wird hier daher angenommen, dass in diesem System (S27) in unserer normalen Umgebung die Elektronen-Bindung stattfindet. Dabei muss uns bewusst bleiben, dass auch eine Überlappung im Feldbereich S9 möglich ist. Dies jedoch wird sehr wahrscheinlich nur im Zentrum eines Sterns stattfinden können, da bei der thermischen Veränderung der Elektronenplätze Neutrinos erzeugt würden anstatt Photonen.
Die Bindungs-Energie
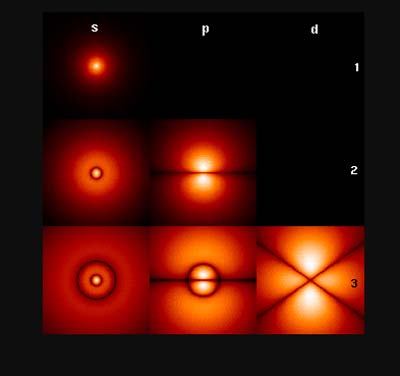 Bild
6 zeigt errechnete Bereiche der Wahrscheinlichkeit nach Schrödinger
Bild
6 zeigt errechnete Bereiche der Wahrscheinlichkeit nach Schrödinger
Allgemein auch Ionisierungsenergie genannt. Diese Energie auf das Periodische System angewandt, zeigt deutlich die Zusammenhänge der 2-er und 8-er Gruppen der Elektronen auf den Schalen um den Atomkern. Erklärt können diese Zusammenhänge durch Kreise auf einer 2D-Ebene nicht wirklich. Dort haben die Valenzelektronen eine schwache Bindungsenergie (p﮲λ), deren Werte auf der einen Seite von ihrer Beziehung zur 8.er Gruppe und zum anderen von ihrer Distanz zum Kern abhängen. Oft wird argumentiert, dass die Elektronen der inneren „Schalen“ im Wege sind, wodurch die Ionisierungsenergie schwächer wird. Das umgekehrte ist jedoch der Fall, wie die Messwerte zeigen. Auch die Anwendung von Orbitale, die Zuordnung von 4 Quantenzahlen, die Berechnungen der Bereiche 90%er Wahrscheinlichkeit mit der Schrödinger-Gleichung sagt nichts über die Werte der Bindungs-Energie der unteren Liste aus.
Bild 7
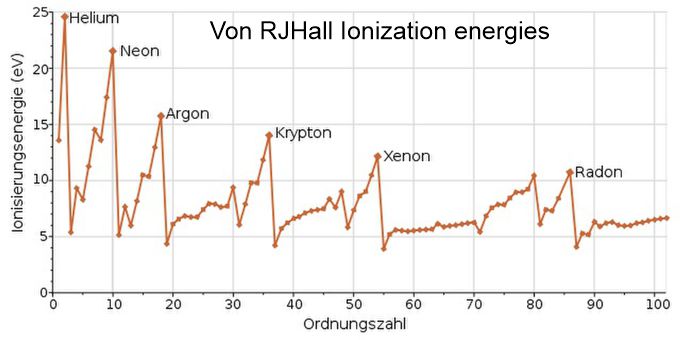
Es sollen hier die experimentellen Werte der Ionisierungsenergien gelten.
A prima Vista sehen wir die periodisch erscheinenden Spitzenwerte, die
in der Tabelle auf die Atomnummer der Edelgase zeigen. Hier 2; 8; 18; 36;
54. Nach Xenon (54) wird es unklar. Die Meinung der Schulphysik, dass die
Ionisierungsenergie vom Abstand zum Atomkern abhängt, ist offensichtlich nur
ein Teil der Wahrheit, weshalb bis jetzt auch kein entsprechendes 3D-Model
dafür gefunden wurde. Die Verteilformel Anzahl Elektronen = 2 x Schale^2
scheint experimentell nicht unterstützt.
Es soll hier kurz auf den
neuesten Stand der Physik hingewiesen werden.
Ein Elektron soll 4
Quantenzahlen (Qn) haben:
Qn 1=n=die horizontale Reihe 1-7 des
periodischen Systems
Qn 2=l=Nebenquantenzahl, die Formen der Orbitale;
l0=s=Kreis; l1=p=Händel; l2=d=gekreuzte Händel.
Qn 3=Magnetquantenzahl
(+) oder (–) in allen 3 Richtungen des 3D-Raumes x;y;z
Qn 4 Spin
Quantenzahl +1/2 oder -1/2.
Dabei macht die Spin-Quantenzahl den größten
Unterschied zur folgenden Erklärung aus der Matrix-Theorie heraus. Die
Schul-Physik benutzt tatsächlich den Spuk einer Doppelbesetzung eines
Raum-Punktes in dem Sinne, dass ein Elektron sich mit einem anderen Elektron
denselben Raumpunkt teilen könnte. Normal sollte man mit Spin eine Drehung
bzw. Rotation meinen. Hier aber wird angenommen, dass ein Elektron von
seiner vollen Rotationszeit 1 nur eine ½ Rotation existiert und Zeit/Raum
der anderen ½ Rotation mit der Existenz eines anderen Elektrons teilen
könne. Das ist unlogisch, da eine Rotation eine Achse hat, die fast
unendlich viele 3D-Winkel haben kann und somit 2 Rotationen sich nie
aufheben. Die Quantenzahl Qn4 wurde offensichtlich erfunden, damit die Schrödinger Formel funktioniert. All diese Quantenzahlen sind daher aus der
Analyse des Aufbaues der Atomhülle entstanden und entsprechen nur ungefähr
der experimentellen Forschung. Um die Idee der Quantenzahlen voll zu ersetzen,
werden hier die 4 Feld-Momente (Paritäten des 720° Zykluses) der Matrix Theorie benutzt.
Anstatt Quantenzahlen gilt hier (++) (+-) (-+) (- -), die 4 Farben der
Matrix.
Die Geometrie der Raum/Zeit Matrix bietet hier eine andere Lösung, die
mit den Ionisierungs-Energien der Elektronen-Hülle übereinstimmt.
Ausgangspunkt sind die Edelgase, die die stabilsten Kombinationen zu sein
scheinen. Die Geometrie der Matrix zeigt hier eine Lösung, wo die
privilegierten Raumpunkte der Atomhülle aus 2-er und 8-er Gruppen besteht.
Diese entstehen durch die Form der Oktaeder, die in der Matrix das schwache
Glied der Raumstruktur bilden. Dies geht aus der Matrix-Theorie hervor, die
für Partikel einen Impact mit Tensor aus 4D annimmt, der dann aus simplen
statischen Gründen einen 3D-Efekt im schwächsten Punkt der Raumstruktur hat.
Die Geometrie der Oktaeder erklärt die Gruppenbildung der
Elektronen-Plätze. Hier die genaue Auflistung:
Atom-Zahl 2 = 2
Atom-Zahl 10 = 2+8
Atom-Zahl 18 = 2+8+8
Atom-Zahl 36 = 2+16 2+16
Atom-Zahl 54 = 2+16 2+16 2+16
Die aktuelle Physik nimmt
an, dass die Orbitale s, p, d usw. aufgefüllt werden. Das aber schafft mit
der (bequemen) Variationsvielfalt eine Menge Edelgas Konfigurationen, was
der Tabelle der Ionisierungsenergien nicht so entspricht. Dort liegen die
Elektronenzahlen energetisch sehr nah beieinander, haben aber beim Übergang
zur Edelgas-Nummer einen abrupten Rücksprung der Bindungsenergie. Diese
Sprünge der Bindungsenergie (Bild 8; Atomnummer 2-3 oder 8-9 usw.) lassen
sich nur durch eine dynamische Komponente des Energiewertes erklären. Die
Physik beschreit es als Magnet-Quanten-Zahl. Es ist ein Wert als
Platz-Füller für die komplette Beschreibung des Elektrons, also eine
Eigenschaft. In der Erklärung der Matrix-Theorie wäre es eine Parität einer
Oszillation. Es ist die alte Geschichte: SPIN oder Parität. Der Matrix-Raum
erlaubt keine Drehung in sich selbst im Quantenmaßstab, da jede Bewegung als
Propagation aufgefasst wird. Die unendlich kleinen Schritte einer Bewegung
würden mit E=hc/λ unendlich hohe Energien und somit ein Paradox erzeugen.
Die Matrix besteht strickt auf eine konsequente geometrische Erklärung. Die
Oszillation des Elektrons mit all seinen Sekundär-Feldern (Para Feldern) schafft
Ladungs-Momente, die sich mit dem zentralen Atomkern aufheben. Solang die
Zahl der Elektronen nicht die des nächst höheren Edelgases (2; 10; 18; usw.)
erreicht hat, wirkt sich das Moment der Ladungs-Oszillation als eine
Unstabilität aus. Beim Zufügen eines neuen Elektrons wird nicht nur der Platz
der besten Symmetrie sondrn auch der stärksten Wechselwirkung (normaler
weise in S1 bis S9 als Gravitation) gewählt. Die Edelgas-Konfiguration hat dann eine
volle-Symmetrie
erreicht.
Der Beta+ Zerfall (ß+)
An Hand des Beta+ Zerfalls, ein Phänomen, das beim Kollaps eines weißen Zwergs eintritt, kann hier der Vorgang so beschrieben werden: Es wird angenommen, dass der Druck im Inneren eines weißen Zwergs so groß wird, dass die Pauli-Barriere von S3 (der Bereich um das Proton mit der Energie eines Elektrons) kollabiert und das Elektron das Parafeld S3 um das Protons besetzt. Das Resultat: Im S3-Bereich und S9 um das Proton werden die Paritäten neutralisiert und es entsteht ein Neutron, ein Proton ohne seine Parafelder (der Ladung, Spiralität usw.).
Das Standart Model: ß+ = p(+) + e(-) = N(o) + e(+) + ν(antineutrino)
das heißt hier:
1 Proton + Elektron wird zum Neutron + Positron + antineutrino
Und mit
der Matrix bzw. der Paritäten der Doppel-Oszillation beschrieben
heißt
das: ß+ = p(++) + e´(+-) + ν´(+-) = N(++) + e(-+) + ν(-+)
Hier wurden die Parafelder von Anfang an mit gezählt. e´(+-) + ν´(+-) sind Parafelder des Protons. Mit dieser Schreibart entstehen keine neuen Partikel, sie werden als frei werdende Energie, als Paritäts-Momente an die Umgebung abgegeben.
Das Standard Model kennt durch die geschichtliche Tradition der zeitlich getrennten Entdeckungen eine Anzahl von Kriterien, die nur schwer zu korrelieren sind. Hier aufgezählt:
Spin --------------------------------- Drehung 720° auf 360° reduziert, daher 1/2 Spin
Chiralität, Helizität ----------------Drehung links-rechts im 3D-Raum (Handregel)
Antimaterie -------------------------alle Quantenwerte (inkl. Zeit) werden umgekehrt
Ladung ------------------------------innere Eigenschaft der Fermions
Immerhin hat Dirac aus dieser Misere seine Spinoren ableiten können. All
diese Werte mit naiven Namen bekamen nun einen mathematischen Zusammenhang.
Auch die Matrix Theorie leitete die 4 Momente im 4D-Raum als Vorzeichen
der Raumdichte ab, (++) (+-) (-+)
(- -) bzw. als Farben
(++) (+-)
(-+) (-
-)
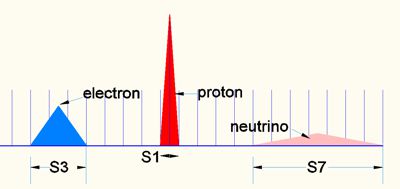 Bild
8
Bild
8
Hier werden die 3 Partikel vom SM (Standart Model) abgeleitet. Vertikal der 4D-Moment (E) und horizontal die relative Feldgröße. Die Werte sind hier symbolisch.
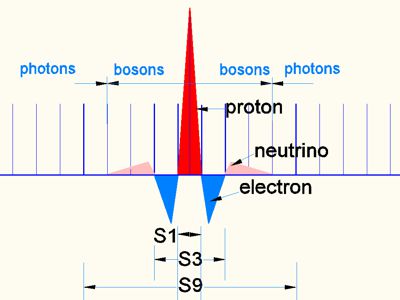 Bild 9
Bild 9
Es zeigt das Proton (rot) mit dem Elektron-Para Feld (blau) und dem Neutrino-Para Feld (hellrot). Parafelder sind die logische Konsequenz der Matrix. Sie entsprechen hier der Formel λC = h / (c · m0) der Compton Wellenlänge.
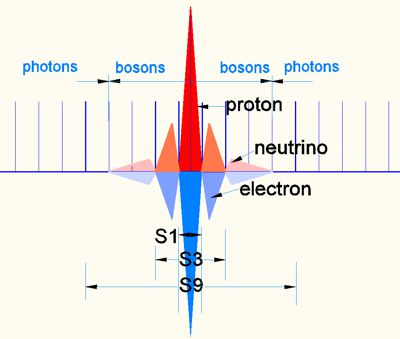 Bild
10
Bild
10
Hier werden die Para Felder des gesamten Zyklus der Doppel-Oszillation gezeigt. Alle Felder und Para Felder heben sich energetisch auf. Dieser Prozess geht in seiner Größe so weit bis im S9 keine Bosonen mehr gebildet werden und EM-Schwingungen von Photonen in den EM-Raum entweicht. Diese Schwingungen sind jedoch neutral und könnten für die dort sehr schwache Gravitation verantwortlich sein.
Die privilegierten Orte in der Matrix
In den nächsten Bildern wird der geometrische Zusammenhang der privilegierten Elektronen-Plätze der Übersichtshalben mit Überschneidungen von 1/3 bzw. 2/3 von S27 dargestellt.
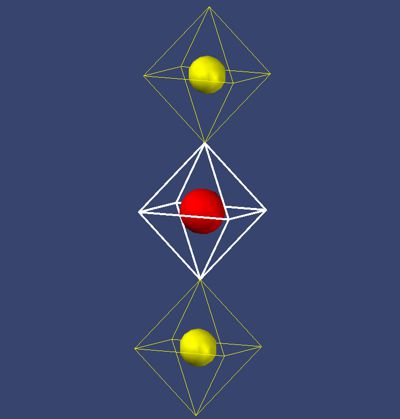
Hier soll ein weiteres Phänomen der Elektronenbindung erklärt werden. Das Andocken des Elektronenfeldes (S9) ist nur ein Teil des Bildes. Wie sicherlich auffallen wird, erzeugt das Andocken gemäß der Matrixtheorie noch keine Anziehung (Abb. 2), sondern nur die Überlappung. Hier überlappt das unsichtbare Feld S27 um 3/9 seiner Kapazität. Wir müssen die Tatsache berücksichtigen, dass die Elektronen hier (gelb) die gleiche Parität haben. Das heißt, Ladung ist nicht die einzige Ursache der Anziehung. Es gibt 2 Kräfte, die Anziehung verursachen: 1. Gravitation 2. Parität oder in der Physik "Ladung" genannt. Gravitation kommt vom 4D-Einfluss und ist in diesen Maßstäben viel stärker als die 3D-Schwingung der Dichte dieser Felder. In großer Entfernung wird ein Elektron viel stärker von der Kraft 1 als von der Kraft 2 angezogen. Das ist der Grund, warum die ersten beiden privilegierten Stellen die Ladungsregel (+/-) nicht anwenden.
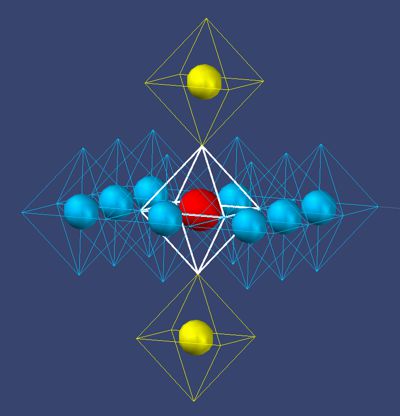
Das Bild zeigt das Neon-Atom mit 10 Elektronen (2+8). Hier soll ein weiterer Aspekt des Verhaltens der Elektronen in der Atomhülle beschrieben werden. Trotz der generellen Anziehung des Atomkerns im Zentrum verhalten sich Elektronen sehr zaghaft in der Wahl ihres Platzes. Das kommt daher, dass die Elektronen sich einen Weg durch die hier nicht dargestellten Sekundarfelder bahnen müssen. Die ganze Dynamik beruht auf Balance. So wird aus der fernen Distanz ein Elektron wellenmäßig angezogen, d.h. es durchläuft (schwache) Zonen der Abstoßung und Anziehung, bis in Nähe des Atomkerns die Täler und Berge so steil werden, dass das Elektron sich in S27 des Atomkerns einpendelt und dort bleibt.
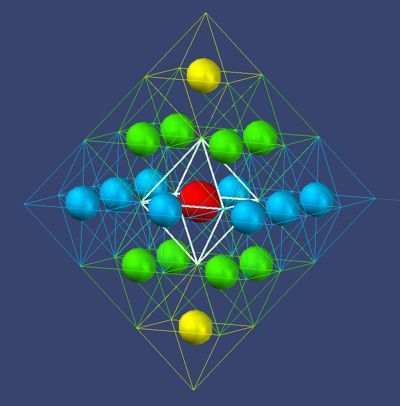
Seine Zusammensetzung ist hier 2+8+8 = 18. Dies erreicht wieder die
Gesamtform als Oktaeder. Als allgemeine Erkenntnis kann die Platz-Wahl der
Elektronen wie folgt gesehen werden: ein Elektron versucht immer zuerst
einen Platz im Feld S27, dass soweit wie möglich von besetzten Plätzen
liegt, jedoch anderseits die möglichst beste Symmetrie bildet. Die beste
Symmetrie resultiert in der Edelgas-Konfiguration. Das danach kommende
Elektron bekommt daher nur einen sehr asymmetrischen Platz, der unstabil ist
und nur einen extrem kleinen Ionisierungs-Wert hat (siehe hier Bild 7).
Zusätzlich als weitere Variable der Attraktion sind die
Bindungs-Kombinationen zu nennen. Hier die Kombinationen der 4 Paritäten als
Momente aus den 4 Dimensionen des Raumes:
(++/+-) (+-/++) (-+/++) (- -/++)
(++/-+) (+-/-+) (-+/+-) (- -/+-)
(++/- -) (+-/-
-) (-+/- -) (- -/-+)
Die Paritäten-Kraft in Kombination mit der
Gravitation ergibt neben der Geometrischen Konstellation die
Ionisierungs-Energie. Die Edelgas-Konfigoration ist die Kombination, wo alle
3 Kräfte ihr Maximum haben, wobei eine Oktaeder Form angestrebt wird.
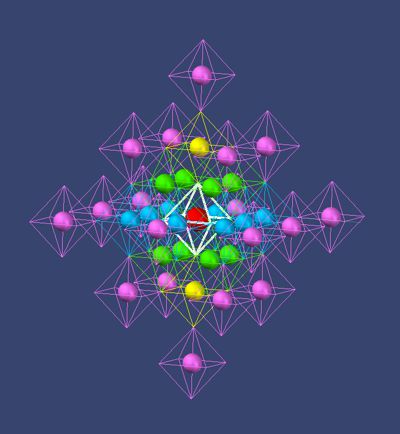 Bild
14 Krypton
Bild
14 Krypton
Seine Elektronenzahl beträgt 36 und sollte geometrisch folgende Abfolge haben: 2; 8; 8; 18. Dargestellt wurden die Elektronen Blau, Grün, Gelb für Argon und Violett für Krypton. Wie in der Ionisierungstabelle gelesen werden kann, sind zuerst 2 Plätze Top und Down gebucht. Danach die 8 Plätze am Äquator (sehr eng liegende Ionisierungsenergien) und zuletzt die Auffüllung Nord- und Süd-Bereich (in immer diagonalen Besetzung entsprechend der Tabelle). Es muss auf die Komplexität des Ladungsfeldes hingewiesen werden, das sich bei jeder weiterer Besetzung als Ganzes ändert.
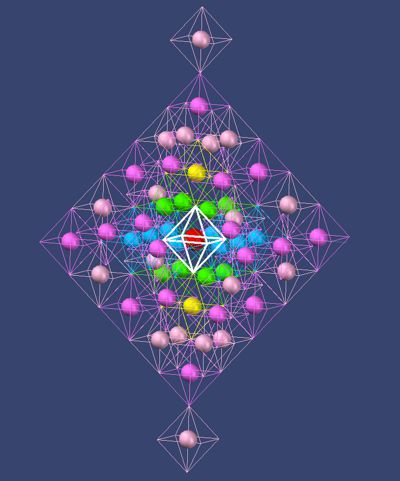
Seine Elektronenzahl beträgt 54 und sollte geometrisch folgende Abfolge haben: 2; 8; 8; 18; 18. Die letzten Gruppen bestehen aus 2 + 8 + 8 = Argon + 2 + 8 + 8 = Xenon, was aus der Ionisierungs-Tabelle (mit einiger Übung) im Detail ablesbar ist. Bis Xenon entsprechen die Edelgasformationen den Reihen des periodischen Systems. Radon wird durch die Reihe der Lanthanoide in seiner Geometrie der Oktaeder gestört und danach endet die Atom-Zahl der natürlichen Elemente vorzeitig. Es wird hier angenommen, dass ein weiterer Layer um den Oktaeder von Xenon potentielle Plätze bereithält. In Theorie der Geometrie des Oktaeders hat der nächste Layer nach Xenon 146 Plätze, wobei 2 Plätze schon vom Xenon besetzt wurden. Die Atomnummern der natürlichen Elemente gehen jedoch nicht soweit. Eine stabile Langlebigkeit kann hier nicht erwartet werden.
Feldüberschneidung 1/3 in S9 im S27 Feldbereich
Theoretisch können Feldüberschneidungen teilweise (1/3) in S9 geschehen. In gleicher Weise können Überschneidungen mit S27 im Feld S81 geschehen. Die Feinstruktur der Matrix für die Oktaeder-Felder verlangt in Theorie, dass Wechselwirkungen als Überschneidung nur in Maßstäben wie S9 oder S27 passieren. Das kommt daher, dass man sich ein Feld als Platzhalter vorstellt, wie ein Tal, das mit Bergen umringt ist. Im Tal aber gibt es eine Feinstruktur, die kleine Vorgebierge in je 1/3 der Schwingungslänge hat. Zustände dieser Art in S9 würde Neutrinos erzeugen. Im Inneren eines Sterns jedoch wäre auch dieser Fall denkbar.
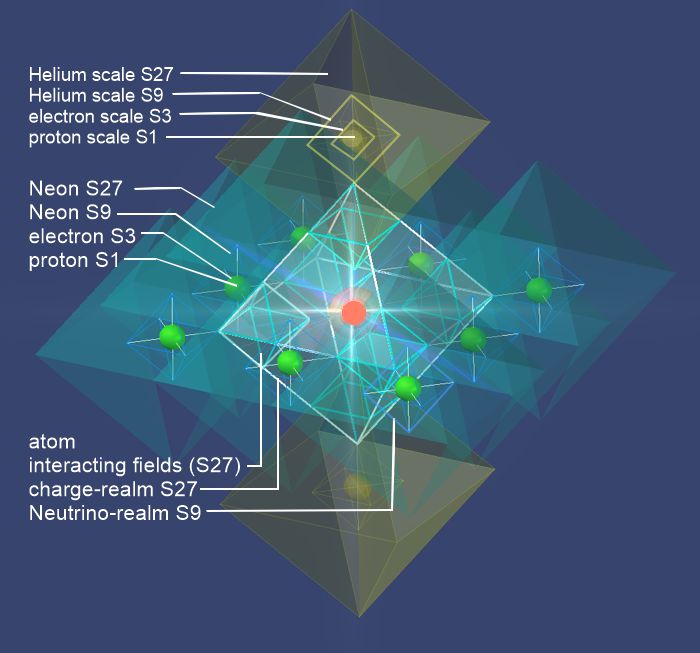
Hier werden die Felder S27 der Elektronen gezeigt. Sehr schwach sind auch die Felder S9 um die Elektronen zu sehen. Der zentrale Oktaeder in weiss ist S27 des Atomkernes. in diesem S27 sind die Überlappungen (kleine weisse Oktaeder in der Grösse S9) erkennbar. Das Bild zeigt hier Neon.
Welche Elemente der Schulphysik können übernommen werden, welche ersetzt?
Die 4 Quantenzahlen können teilweise übernommen oder ersetzt werden.
Wert Qn1 – Qn7 entsprechen den 7 Gängen des Füllens der
geometrischen Plätze in der Oktaeder-Matrix (5 Farben zun Xenon) und auch den Stockwerken des Periodischen
Systems.
Wert Qn2=l kann nicht übernommen werden, da sie
der Vorstellung eines dynamisch bewegten Systems entsprechen. Die Frage
stellt sich, ob Q2=l nötig ist, ein einfacher Blick ins Periodische System
sagt ja alles.
Wert Qn3=magnet-Quant
wird durch das
Drehmoment des ganzen Systems ersetzt werden. Dabei gilt, dass die asymmetrischen
Plätze, die mit ihrer Auffüllung den Schwerpunkt gegenüber dem geometrischen
Schwerpunkt ändern, ein Moment (Vibration) erzeugen. Es entsteht eine
Schwäche der Bindung. Auch hier sagt die
Ionisierungs-Energie alles.
Wert Qn4=Spin. Dieser Wert
entfällt, da die Formel Qn1 x (Qn2)^2 bewiesener Weise nicht stimmt. Da der
Spin eine Achse erzeugt und diese sich bei jedem neuen Elektron anpassen
müsste, wird die Sache paradox. Einfacher ist die oben begründete Parität,
die so auch im Experiment Stern Gerlach das gleiche Resultat erzeugen würde.
Die Parität einer Oszillation des Elektrons aber wäre eine Funktion des
Raumes selbst. Die schwierige Achsenvorstellung im Quantensalat wäre nicht
nötig.
Es soll hier erinnert werden, dass in der Raum-Matrix alle Oktaeder nur
„leere“ Abstände der Tetra-Struktur des Raumes sind und als schwächstes
Glied des Mediums „Raum“ die Impulse aus der 4. Raumdimension aufnehmen. Das
ist der Grund, dass Fermionen (hier die Elektronen) das Zentrum von Oktaeder
sind. Der Oktaeder selber ist das erste Feld. Weitere Felder (Para-Felder) bis hin zu den
Feldern der „Ladung“ sind wieder Oktaeder, die symmetrisch um das
Original-Feld liegen. Das alles oszilliert in Harmony zu allen Oszillationen
im Raum.
Die Oszillation der
Elektronen in der Matrix haben immer und überall in der Raum-Matrix
Gegenparität zum Proton. Alle „leeren“ Umgebungs-Raumzellen oszillieren
überall als Tetraeder in 4 Paritäten=>
(++) (+-) (-+) (- -)
Für ein tieferes Verständnis zur Matrix-Theorie empfehle ich meine weiteren Schriften.
die Matrix des Weltmediums
Die Schwingung des Welt-Mediums
die Geometrie des Mediums Raum
Das Universum
Friedmann-space and the space-matrix
Das Raum-Zeit-Kontinuum
Die Raum-Zeit-Illusion
Teilchen in der Matrix Struktur
Das Elektron
Gunter Michaelis,
Griesbach den 27.2.2023 rev. 02.01.25